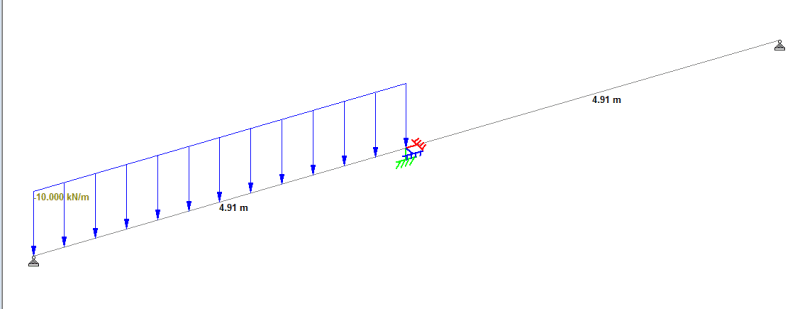
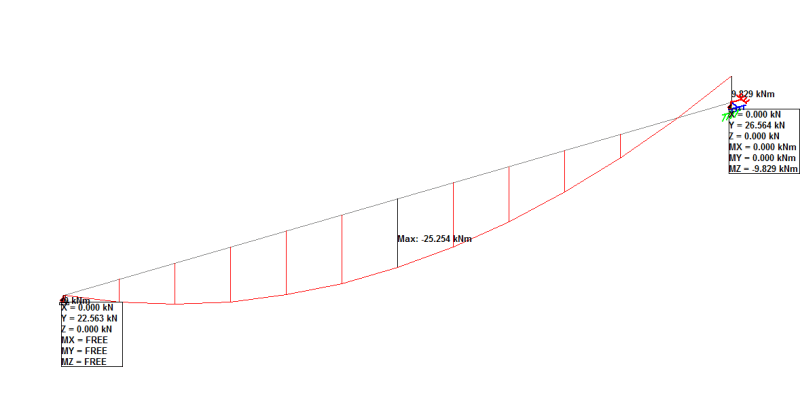
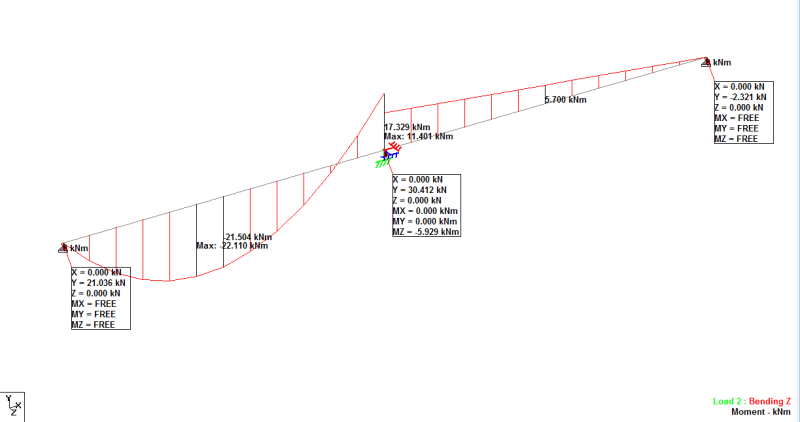
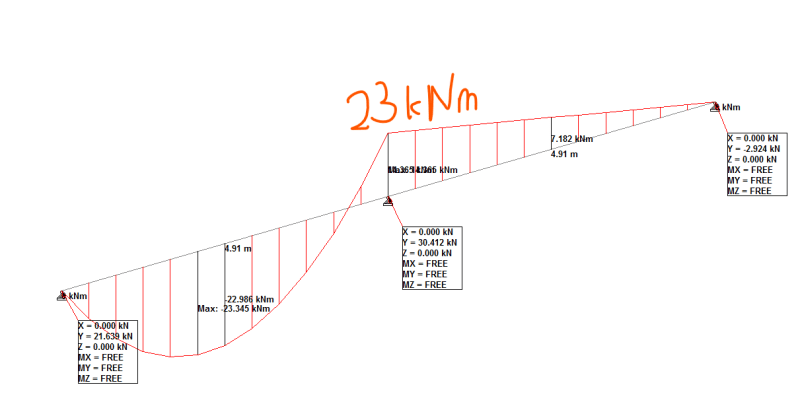
We all know that the continuous beam is generally stiffer, hence , the interior support can attract a fair value of hogging moment.
I am playing around with the spring rotation value to limit the hogging moment reaction to certain amount (lower value compared to all fixed condition). However, I found that when the beam is in continuous , the amount of spring value that required to achieve certain amount of reaction moment at support is lower. Is it wrong ? Why ?
Can someone help to explain it ? Say that when in all fixed condition, the reaction moment at interior support is 300kNm, but I want to limit it to 100kNm only. Hence, I adjust the spring value to achieve it. In single span fixed fixed condition, the spring value is 100kNm /deg , but in continuous fixed-fixed-fixed condition, the spring value is 50kNm /deg. Why ?
I am playing around with the spring rotation value to limit the hogging moment reaction to certain amount (lower value compared to all fixed condition). However, I found that when the beam is in continuous , the amount of spring value that required to achieve certain amount of reaction moment at support is lower. Is it wrong ? Why ?
Can someone help to explain it ? Say that when in all fixed condition, the reaction moment at interior support is 300kNm, but I want to limit it to 100kNm only. Hence, I adjust the spring value to achieve it. In single span fixed fixed condition, the spring value is 100kNm /deg , but in continuous fixed-fixed-fixed condition, the spring value is 50kNm /deg. Why ?


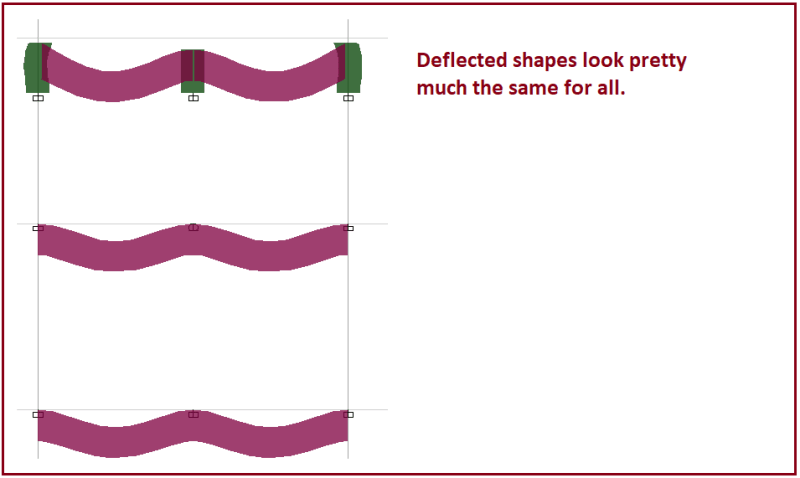
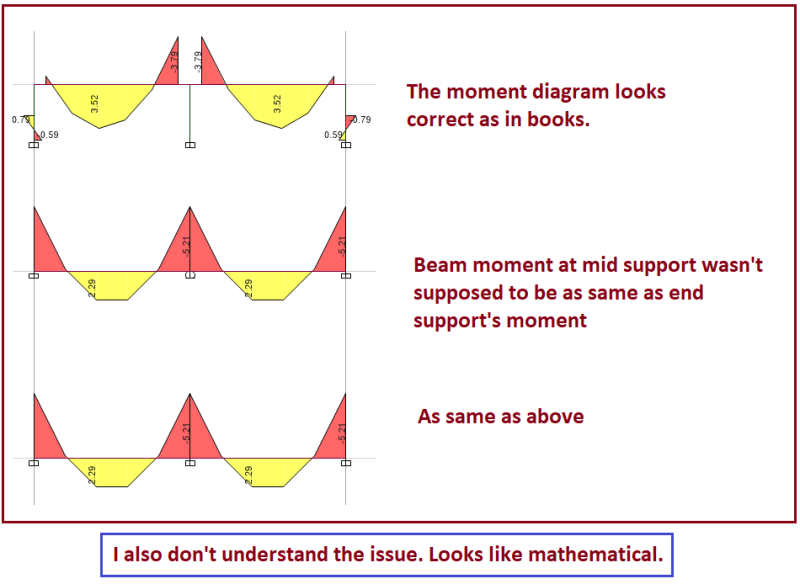
![[ponder] [ponder] [ponder]](/data/assets/smilies/ponder.gif)