Steel Angle Question 2

[CorporalToe]

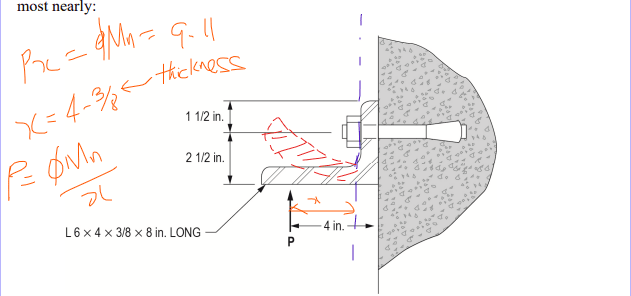
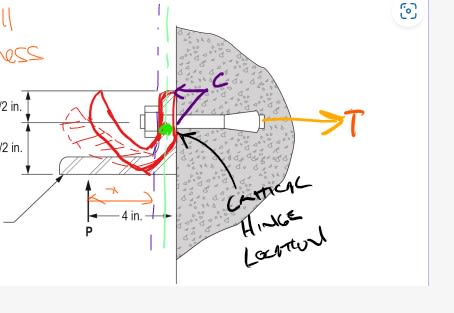
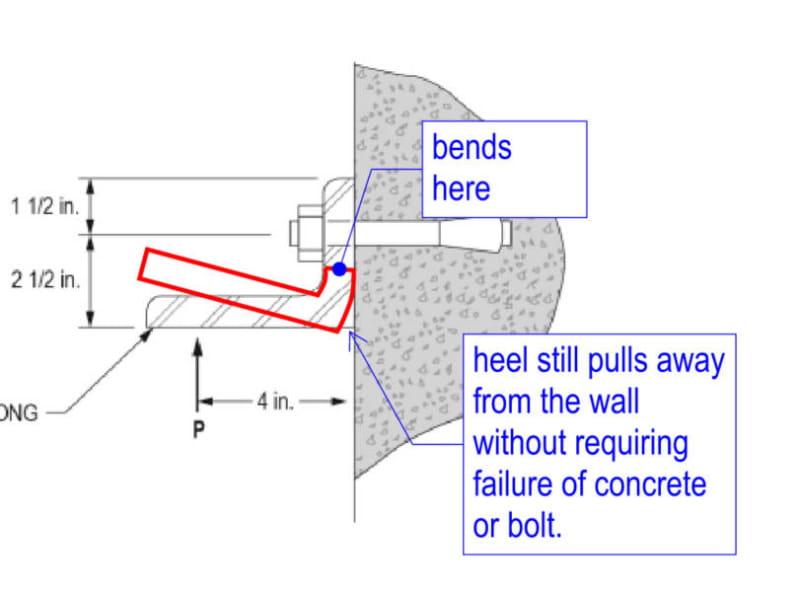
Hello I am studying for my PE Civil Structural Exam. I was wondering for this question why would you not use the yielding formula from
AISC 360-16 F.10:

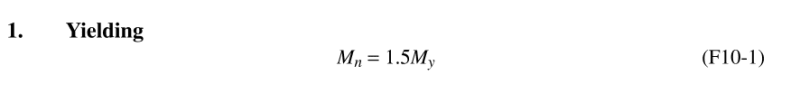
Question:

Solution:

 

[Greenalleycat]

I'm a bit confused by your question

The calculations you've provided have My = 1/6bd2 and Mp = 1/4bd2 - isn't that incorporating the 1.5x factor?
This is based on whether your critical point (angle leg moment capacity in this case) is likely to be subject to local buckling or whether it can achieve a full section plastic capacity
It's not guaranteed that every section can do this, though I typically do make this assumptions for angles

 

[CorporalToe]

So F.10 says that Mn = 1.5My, I do not understand why they didn't just use this instead they used Mn = Mp <= 1.6My. Why use this? I see that in F.11 for rectangular bars and rounds they use Mn = Mp <= 1.6My, but why use this for angles? Sorry if this is hard to understand.

 

[driftLimiter]

The flexure is about a single leg of the angle. The formula you posted is for flexure of the gross cross section.
A single leg of the angle in flexure is treated like a rectangle, this would send us to AISC F11.

 

[jdcollins]

The first equation you post from F10-1 is for single single angles loaded along their length. The situation you have in the problem is for the bending of a single leg of the angle, which effectively behaves as a rectangular bar, which is controlled by section F11 in AISC. You'll see that the Yielding equation in that section is Mn = Mp = FyZ ≤ 1.6My.

 

[CorporalToe]

Just a follow up at the end why did they divide the moment by 4-3/8? I know the answer is suppose to be P but I am confused how dividing it by that gives P?

 

[Greenalleycat]

9.11 is the moment capacity, right?
But it's the moment capacity at the critical section within the leg of the angle
The force P is dimensioned as 4" from the face of the concrete, but the leg of the angle starts 3/8" short of that
So you get a small bump in max force allowed

 

[BulbTheBuilder]

 

[lexpatrie]

That "by inspection P controls" has me lost. What does that even mean, is there some other criteria I'm supposed to dismiss out of hand?

The 1.5My is for bending along the length of the angle. That's why they didn't use it.

 

[BulbTheBuilder]

Something I am now noticing, why is 8" used as b in computing section modulus not 6"?

 

[driftLimiter]

The length of the angle is 8" they are using the full length as the width of the bending flange.

 

[BulbTheBuilder]

oh I see, thanks

[Edit]
But isn't the modulus a cross-sectional property? I was thinking the 8" would be used for flexural (EI) rather.

 

[Celt83]

I would argue the proposed solution is incorrect for the shown configuration, the critical bend plane is actually in the vertical leg. The load configuration shown will cause the angle heel to pull away from the wall and the vertical leg will bend about the anchor.

So the critical value for P should be 9.11 in-kips / (4 in-(3/16 in)) = 2.39 kips. where 3/16" comes from 1/2 * 3/8 in.

 

[driftLimiter]

Bulb, the section being analyzed in the example is the rectangualar section of the bottom leg in bending.

The problem has us thinking about the single leg of the angle resisting bending like a cantilever. That leg has it's own cross-section properties (S,Z,I,etc)

In this problem, the rectangualar cross-section is 8" wide and 3/8" thk.

 

[BulbTheBuilder]

Thank you, driftlimiter. I can see clearly now

 

[EngDM]

I would argue the proposed solution is incorrect for the shown configuration, the critical bend plane is actually in the vertical leg. The load configuration shown will cause the angle heel to pull away from the wall and the vertical leg will bend about the anchor.

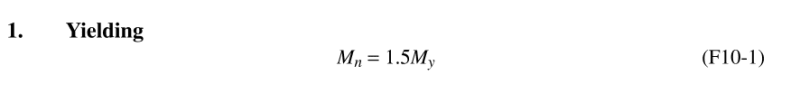
The question states assumptions that the anchor is sufficient and the concrete is sufficient. They could have worded it better but its presented as the vertical leg stays put.

 

[Celt83]

neither of those assumptions precludes bending in the vertical angle leg.

 

[dold]

I agree with celt. Niether bolt nor concrete need to fail for the heel to move away from the wall.

damn he beat me to it.

 

[BulbTheBuilder]

Celt, will the proposed solution be valid assuming it was rigid and there's no rotation at the anchored end?

 

[BulbTheBuilder]

Looking back at it...I am not making any sense, and the heel does "detach" from the wall. This is my cue to clock out...