I am trying to clarify J10.4 in AISC - Web Sidesway Buckling. I might be a little picky here, but I want to make sure I understand this correctly.
AISC gives two different equations depending on whether or not the compression flange is restrained against rotation. Here is my confusion:
J10.4 -
"This section applies only to compressive single-concentrated forces applied to mem-
bers where relative lateral movement between the loaded compression flange and the
tension flange is not restrained at the point of application of the concentrated force."
J10.4a
"If the compression flange is restrained against rotation"
J10.4b
"If the compression flange is not restrained against rotation"
"When the required strength of the web exceeds the available strength, local
lateral bracing shall be provided at both flanges at the point of application of the
concentrated forces."
Comm J10.4
"The web sidesway buckling provisions (Equations J10-6 and J10-7) apply only to
compressive forces in bearing connections and do not apply to moment connections.
The web sidesway buckling provisions were developed after observing several unex-
pected failures in tested beams (Summers and Yura, 1982; Elgaaly, 1983). In those
tests, the compression flanges were braced at the concentrated load, the web was sub-
jected to compression from a concentrated load applied to the flange, and the tension
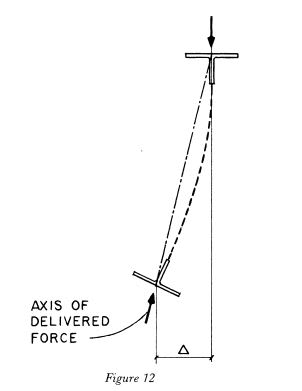
flange buckled (see Figure C-J10.2)."
Comm J10.4a
"For flanges restrained against rotation (such as when connected to a slab), when.."
Comm J10.4b
"For flanges not restrained against rotation, when"
Alright, so my questions:
[ol 1]
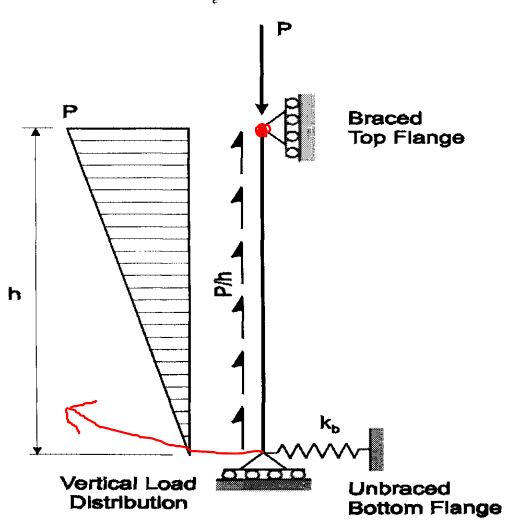
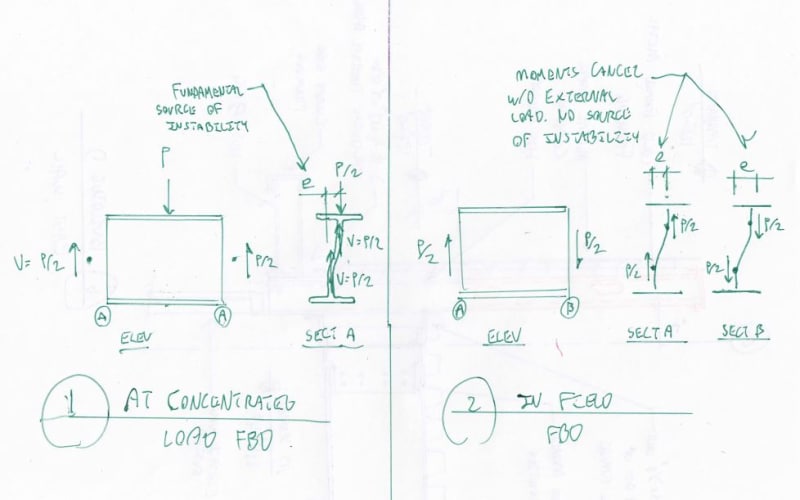
[li]In my first snippet AISC states this limit states only applies to beams where relative lateral movement between flanges is not restrained. However, Figure C-J10.2 (or J10.3 depending on edition) defines the unbraced lengths used in the web sidesway buckling equations. The last figure shows the top and bottom flange braced at the location of the concentrated load and defines the unbraced flange length as L/2. Shouldn't the limit state not apply?[/li]
[li]AISC states for flanges "restrained against rotation", do they mean - the local compression flange is restrained against rotation or the entire section is restrained against rotation? Or do they mean that the compression flange is restrained against lateral translation? In figure CJ10.1 they show the compression flange as being braced against lateral translation. Also in the commentary they state "(such as when connected to a slab)".[/li]
[li]Would this apply to the end of a uniformly loaded beam? I want to say no, because it states the "loaded compression flange". In the case of the end of a beam, you would have a "loaded tension flange".[/li]
[/ol]
Thanks!
EIT
AISC gives two different equations depending on whether or not the compression flange is restrained against rotation. Here is my confusion:
J10.4 -
"This section applies only to compressive single-concentrated forces applied to mem-
bers where relative lateral movement between the loaded compression flange and the
tension flange is not restrained at the point of application of the concentrated force."
J10.4a
"If the compression flange is restrained against rotation"
J10.4b
"If the compression flange is not restrained against rotation"
"When the required strength of the web exceeds the available strength, local
lateral bracing shall be provided at both flanges at the point of application of the
concentrated forces."
Comm J10.4
"The web sidesway buckling provisions (Equations J10-6 and J10-7) apply only to
compressive forces in bearing connections and do not apply to moment connections.
The web sidesway buckling provisions were developed after observing several unex-
pected failures in tested beams (Summers and Yura, 1982; Elgaaly, 1983). In those
tests, the compression flanges were braced at the concentrated load, the web was sub-
jected to compression from a concentrated load applied to the flange, and the tension
flange buckled (see Figure C-J10.2)."
Comm J10.4a
"For flanges restrained against rotation (such as when connected to a slab), when.."
Comm J10.4b
"For flanges not restrained against rotation, when"
Alright, so my questions:
[ol 1]
[li]In my first snippet AISC states this limit states only applies to beams where relative lateral movement between flanges is not restrained. However, Figure C-J10.2 (or J10.3 depending on edition) defines the unbraced lengths used in the web sidesway buckling equations. The last figure shows the top and bottom flange braced at the location of the concentrated load and defines the unbraced flange length as L/2. Shouldn't the limit state not apply?[/li]
[li]AISC states for flanges "restrained against rotation", do they mean - the local compression flange is restrained against rotation or the entire section is restrained against rotation? Or do they mean that the compression flange is restrained against lateral translation? In figure CJ10.1 they show the compression flange as being braced against lateral translation. Also in the commentary they state "(such as when connected to a slab)".[/li]
[li]Would this apply to the end of a uniformly loaded beam? I want to say no, because it states the "loaded compression flange". In the case of the end of a beam, you would have a "loaded tension flange".[/li]
[/ol]
Thanks!
EIT


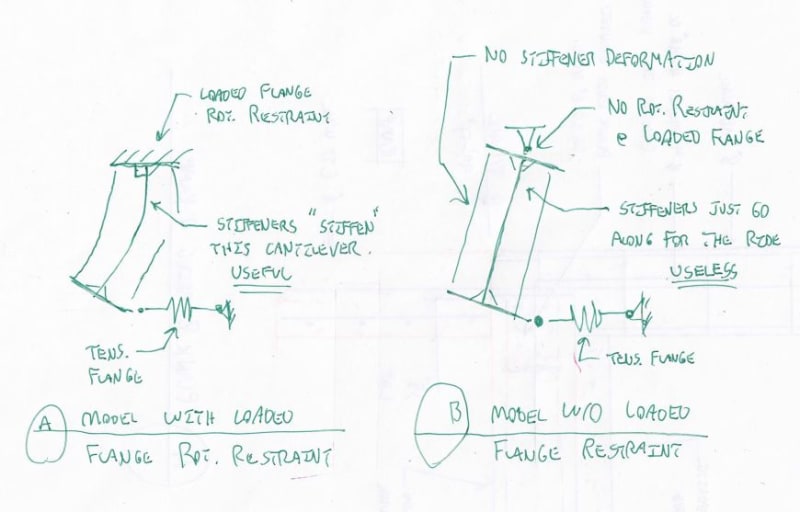

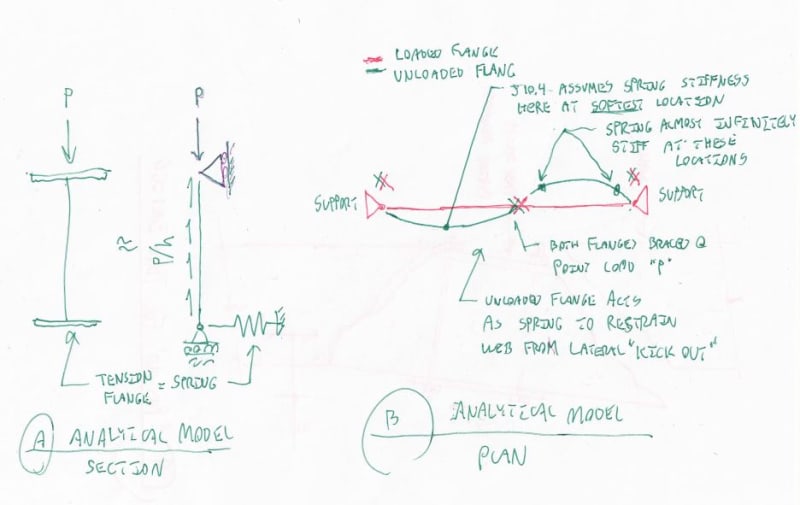


![[smile] [smile] [smile]](/data/assets/smilies/smile.gif) Doesn't fit either of our interpretations.
Doesn't fit either of our interpretations.