MechE123abc
Mechanical
- May 10, 2024
- 1
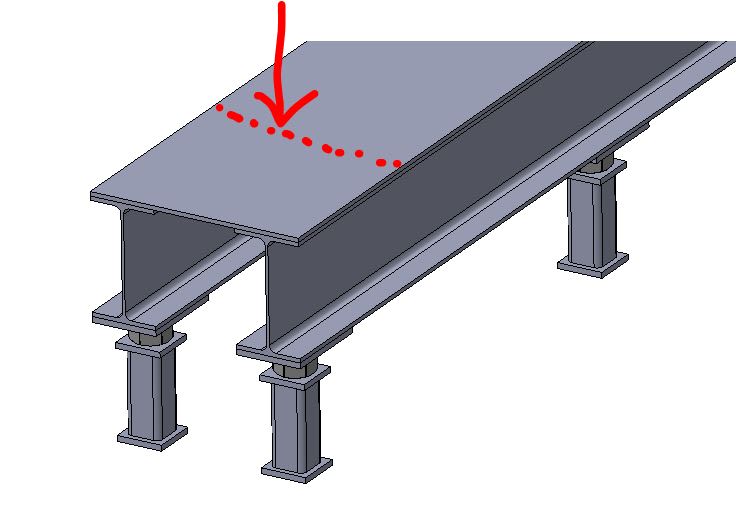
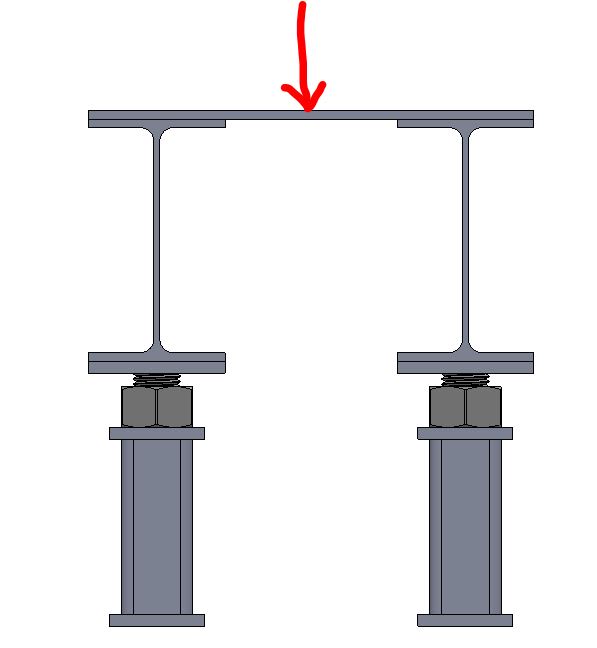
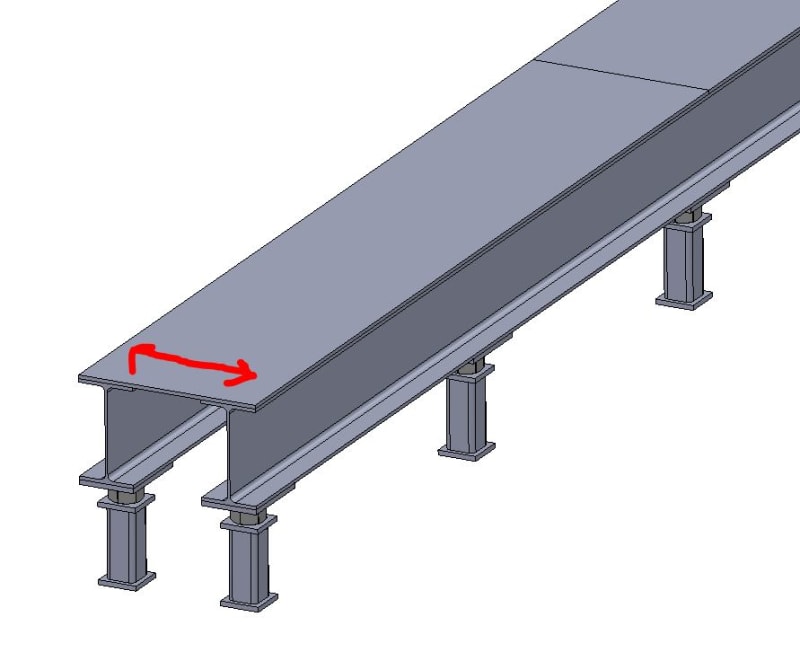
It's been a while since I've done structural stress analysis so feel free to explain as much as necessary. I am building this structure to act as a raised floor. The steel plate will screw into the flanges of the W-beams. I want to perform stress analysis on this top steel plate to determine if it will fail under certain loads. Let's say there's a point load of 10,000 lbs in the middle of the plate (where it's unsupported underneath) as shown in the pictures. From what I remember, I can check for bending stress and shear stress. If I take the two W-beams as the pinned supports with the span being shown in the third picture, I can determine max shear forces and max bending moments. However, what would I use as the cross section? I assume one dimension would be the height/thickness of the plate but would the other dimension be the full long side length of the plate? For example, if the thickness of the plate is 3/8" and the long length is 94" would the section modulus be 2.203 in^3? Not sure if I'm even evaluating this correctly.