MegaStructures
Structural
- Sep 26, 2019
- 376
Hello,
I need some help determining the stress in a "stiffening beam" at service level loads. At the service level moment, the concrete is uncracked. I'm not exactly sure why, but the fact that the concrete is uncracked has made this analysis extremely confusing to me, so I wanted to get a confirmation that my method is accurate.
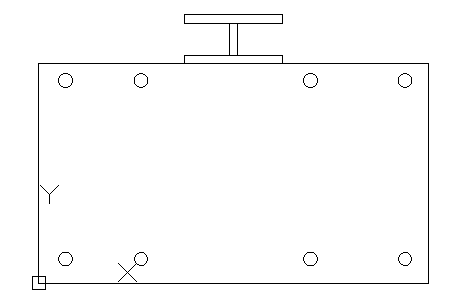
So, I have a concrete beam with rebar on bottom and top and an additional steel reinforcing beam anchored to the top of the concrete beam. I have created a detailed FEM that shows the force in the steel beam, and I am trying to develop a hand calculation to verify my results. I believe what I need to do is the following:
[ol i]
[li]Calculate transformed areas of rebar and steel beam[/li]
[li]Find centroid of composite section using the moment area method[/li]
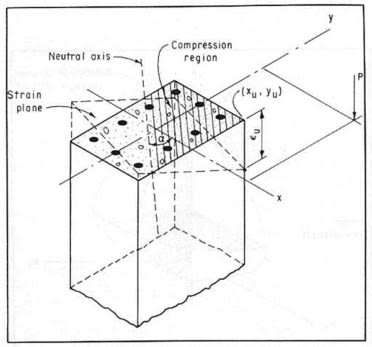
[li]Calculate the transformed moment of inertia using the calculated centroid, since concrete is uncracked I would use the entirety of the concrete as part of the MOI, not just the compression side[/li]
[li]Calculate stress as sigma=MY/I, since the section is elastic[/li]
[li]Calculate the force in the stiffening beam by multiplying the area of the stiffening beam by the stress at the extreme fiber of it[/li]
[/ol]
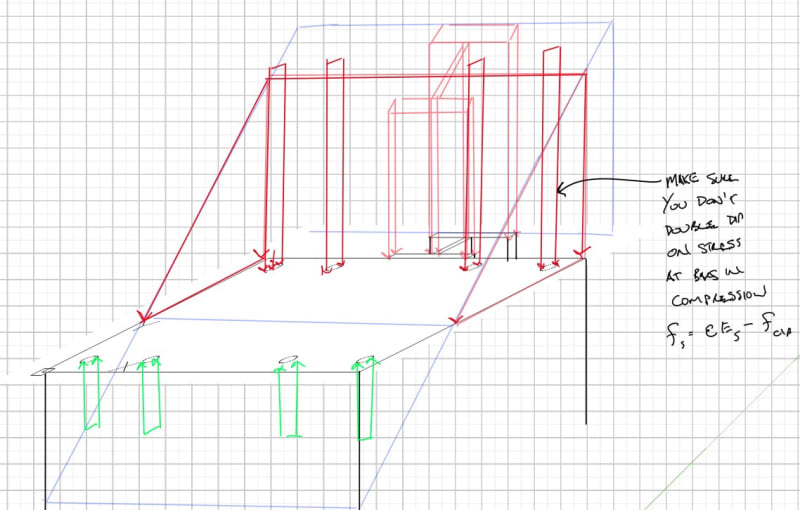
One of the difficulties I am having is that when I do this I am not getting the forces in the cross section to balance out. I am including forces for all rebars, the stiffening beam, the compressive component of concrete, and the tensile component of concrete. A couple things I'm wondering is:
[ol i]
[li]Should the Whitney stress block be used at strains less than 0.003, or is the stress-strain relationship of concrete significantly different at this point?[/li]
[li]Should I calculate the area under the stress diagram as a trapezoid instead of a rectangle (account for reduction in stress at the bottom of the stiffening beam)?[/li]
[/ol]
And now finally I must ask if there is a different method that I should be using instead and is there a excel file or other reference that I can use as a tool for checking my work and speeding up the analysis process?
“The most successful people in life are the ones who ask questions. They’re always learning. They’re always growing. They’re always pushing.” Robert Kiyosaki
I need some help determining the stress in a "stiffening beam" at service level loads. At the service level moment, the concrete is uncracked. I'm not exactly sure why, but the fact that the concrete is uncracked has made this analysis extremely confusing to me, so I wanted to get a confirmation that my method is accurate.
So, I have a concrete beam with rebar on bottom and top and an additional steel reinforcing beam anchored to the top of the concrete beam. I have created a detailed FEM that shows the force in the steel beam, and I am trying to develop a hand calculation to verify my results. I believe what I need to do is the following:
[ol i]
[li]Calculate transformed areas of rebar and steel beam[/li]
[li]Find centroid of composite section using the moment area method[/li]
[li]Calculate the transformed moment of inertia using the calculated centroid, since concrete is uncracked I would use the entirety of the concrete as part of the MOI, not just the compression side[/li]
[li]Calculate stress as sigma=MY/I, since the section is elastic[/li]
[li]Calculate the force in the stiffening beam by multiplying the area of the stiffening beam by the stress at the extreme fiber of it[/li]
[/ol]
One of the difficulties I am having is that when I do this I am not getting the forces in the cross section to balance out. I am including forces for all rebars, the stiffening beam, the compressive component of concrete, and the tensile component of concrete. A couple things I'm wondering is:
[ol i]
[li]Should the Whitney stress block be used at strains less than 0.003, or is the stress-strain relationship of concrete significantly different at this point?[/li]
[li]Should I calculate the area under the stress diagram as a trapezoid instead of a rectangle (account for reduction in stress at the bottom of the stiffening beam)?[/li]
[/ol]
And now finally I must ask if there is a different method that I should be using instead and is there a excel file or other reference that I can use as a tool for checking my work and speeding up the analysis process?
“The most successful people in life are the ones who ask questions. They’re always learning. They’re always growing. They’re always pushing.” Robert Kiyosaki