AR2_Struc
Structural
- Nov 15, 2022
- 3
I have a situation where I'm placing a 24" strongwall at the end of a wood beam. Overstrength forces bring the uplift/compression to 34-kips, requiring a Wide Flange beam. The strongwall is secured to the top flange of the beam with web stiffeners provided.
Given the proximity of the strongwall to the beam support (in this case an HSS column), a fellow engineer believes that the 34-kip uplift needs to be transferred directly to the column since the load will 'follow the path of least resistance'. I am in disagreement with this and believe that the beam will dissipate this force significantly through 'beam action', shown by the attached free body diagram. I argue that since the strongwall is securely anchored to the beam and not directly to the column, I should design the connection for the beam reaction and not the direct uplift force from the strongwall.
Any thoughts?
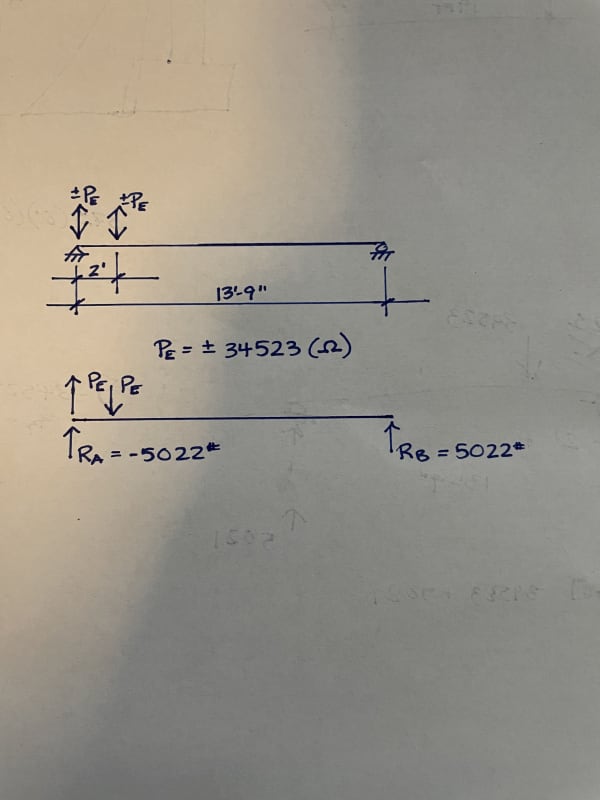
Given the proximity of the strongwall to the beam support (in this case an HSS column), a fellow engineer believes that the 34-kip uplift needs to be transferred directly to the column since the load will 'follow the path of least resistance'. I am in disagreement with this and believe that the beam will dissipate this force significantly through 'beam action', shown by the attached free body diagram. I argue that since the strongwall is securely anchored to the beam and not directly to the column, I should design the connection for the beam reaction and not the direct uplift force from the strongwall.
Any thoughts?

