MatthewMansfield
Civil/Environmental
Hello all
Please dont shoot me down for asking this question as I know it maybe simple for most people.
I am trying to remove doubt from my mind regarding the 3 x types of supports and their reactions.
To me the types of support and their reaction forces are:-
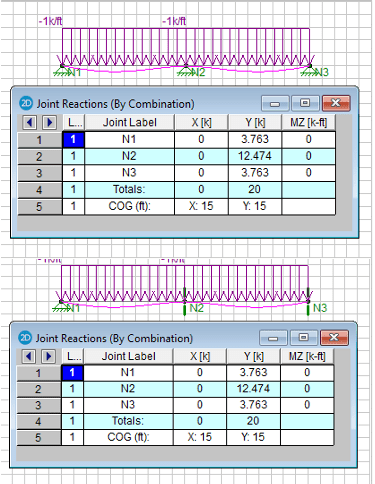
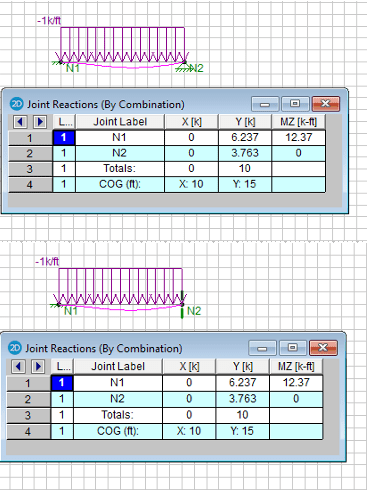
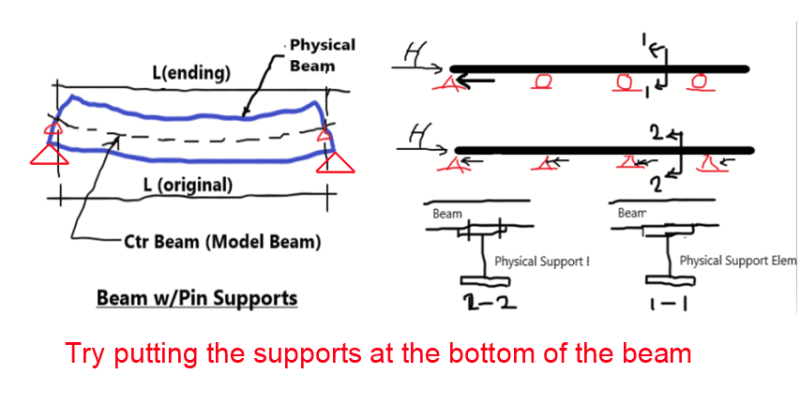
Fixed Support = Vertical Reaction, Horizontal Reaction, Bending Moment Reaction.
Hinged Support = Vertical Reaction, Horizontal Reaction.
Roller Support = Vertical Reaction, Bending Moment Reaction.
To me the above supports can ONLY have those reaction forces - would this be correct?
The reason I ask is because someone told me that a roller support does NOT have a bending moment reaction and i was immediately thrown into confusion.
Can anyone confirm?
Thank you.
Please dont shoot me down for asking this question as I know it maybe simple for most people.
I am trying to remove doubt from my mind regarding the 3 x types of supports and their reactions.
To me the types of support and their reaction forces are:-
Fixed Support = Vertical Reaction, Horizontal Reaction, Bending Moment Reaction.
Hinged Support = Vertical Reaction, Horizontal Reaction.
Roller Support = Vertical Reaction, Bending Moment Reaction.
To me the above supports can ONLY have those reaction forces - would this be correct?
The reason I ask is because someone told me that a roller support does NOT have a bending moment reaction and i was immediately thrown into confusion.
Can anyone confirm?
Thank you.