markboc
Bioengineer
- Sep 1, 2020
- 19
Greetings!
Hopefully you can enlighten me on the following problem. Image a situation like depicted in the drawing. For the pump I'd like to calculate a system curve, so basically stream 1 and 3. I have trouble incorporating stream 2 into the equation for the following reasons:
- Stream 2 has a different density than Stream 1
- Stream 2 is a utility / mains line (think water), hence it is not feasible for me to get a clear of the piping / pump for stream 2
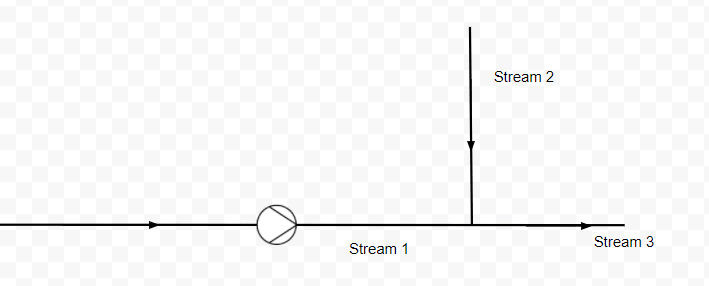
1 ) How will the different density of the mixture (I kept the PID simple, after merging both streams there's a mixer) influence the system curve? I know that for a single medium the density does not matter as we are speaking of pressure in terms of equivalent heights.
2) The utility stream with its inherent pressure will also create a flow, how does that influence the system curve?
My ideas:
Premise: I used MS Excel to calculate the pressure losses across individual piping segments and thus create my system curve.
1) For the initial calculation of my system curve, I will add the flow of Stream 2 to each of my pressure loss calculations for Stream 1 after merging. E.g. if the pressure loss for a flowrate of Q1 was calculated as H = f(Q1) for Stream 1 it is now H = f(Q1+Q2) for Stream 3
2) At the t-junction the pressure should be equal for Stream 1 and Stream 2 to avoid reverse flow.
All flows are liquid, the densities vary by a factor of 2 at most. Stream 2 flowrate may vary between 1.5 to 20 times Stream 1 flowrate.
If anyone could give me pointers in the right direction or what assumptions may be valid I'd be very grateful.
Hopefully you can enlighten me on the following problem. Image a situation like depicted in the drawing. For the pump I'd like to calculate a system curve, so basically stream 1 and 3. I have trouble incorporating stream 2 into the equation for the following reasons:
- Stream 2 has a different density than Stream 1
- Stream 2 is a utility / mains line (think water), hence it is not feasible for me to get a clear of the piping / pump for stream 2
- however I know the desired volumen flow of Stream 2 and I can probably find out its pressure
- and I also thought parallel pump calculations (known) are restricted to pumps with a shared suction side

1 ) How will the different density of the mixture (I kept the PID simple, after merging both streams there's a mixer) influence the system curve? I know that for a single medium the density does not matter as we are speaking of pressure in terms of equivalent heights.
2) The utility stream with its inherent pressure will also create a flow, how does that influence the system curve?
My ideas:
Premise: I used MS Excel to calculate the pressure losses across individual piping segments and thus create my system curve.
1) For the initial calculation of my system curve, I will add the flow of Stream 2 to each of my pressure loss calculations for Stream 1 after merging. E.g. if the pressure loss for a flowrate of Q1 was calculated as H = f(Q1) for Stream 1 it is now H = f(Q1+Q2) for Stream 3
2) At the t-junction the pressure should be equal for Stream 1 and Stream 2 to avoid reverse flow.
All flows are liquid, the densities vary by a factor of 2 at most. Stream 2 flowrate may vary between 1.5 to 20 times Stream 1 flowrate.
If anyone could give me pointers in the right direction or what assumptions may be valid I'd be very grateful.