Thin Plate in tension only

[kphillips]

We are looking at analyzing a panel as a thin plate. The thin plate has load applied to its perpendicular face. The panel is supported by members at various lines along its length. Every analysis we run indicates that the thin plate has a moment from the load applied, but the thin plate is really acting as a tension member. Can the moment in a thin plate be ignored and we just look at the tension in the plate? Any input would be greatly appreciated.

Thank you

 

[strucbells]

Provide a sketch. From your description, it sounds like moment would occur, but it's hard to tell without a visual.

 

[kphillips]

Here is the model that we are working with. Right now the moment contour is turned on.

 

[dold]

I'm not sure of the scale of your plate, but the phenomenon you're talking about requires a non-linear analysis. You won't get any axial loads in your plates due to out of plane loads using first-order analysis alone. There are ways to approximate this in RISA with members (modeling a sagging cable, for exmaple) but i've never tried that with plates.

 

[JStephen]

This assumption is made in the roof plates of large storage tanks. In that case, some rules-of-thumb are also used to limit the spans.
Roark has some design cases for large deflection using a membrane-only analysis in circular plates.
Generally, if the calculated deflection in a bending analysis is larger than half the plate thickness, then the tension forces in the plate also need to be considered.
Assuming the load is carried by tension in the plate, then whatever is around the edges of that plate has to be stiff enough and strong enough to support the load based on the assumptions used.
Neglecting the moment may be conservative when checking for the strength of the plate, but the moment is still there, and you could get permanent deflections in the plate, which may or may not be objectionable.
I think you could also get buckles or waves in the plate under the right conditions.
If the load can be fully reversed, watch out for fatigue.

 

[JoshPlumSE]

dold has it right. This is not something that RISA can do.... at least not without a lot of work on your part. Maybe not even then.

The basic problem is that RISA is not currently capable of accounting for geometric non-linearity in plate analysis. I think of this as the "Trapeze artist" for 1D elements (like beams) or the "trampoline" problem for 2D elements (like plates).

When the trapeze artist gets ready to step on the high wire, it is nominally straight (and let's pretend the tension in the wire is zero). The RISA analysis is based on small deflection theory, meaning that the assumption is the deflection doesn't alter the stiffness matrix at all. So, the initial stiffness of the wire is merely it's moment of inertia and the wire deflects. In reality, tension will develop in the wire to resist the downward deflection. But, this is a non-linear effect that requires consideration of the DEFLECTED geometry in the stiffness matrix.

The same basic concept holds for the "trampoline effect" on flat plate models.

For 1D elements like beams, you can "approximate" the behavior if you first do a hand calc and enter in your anticipated final geometry of the beam as if that's the initial un-deflected shape. The challenge with this is that you may need to have a different geometry for every load case you want to run.

It gets even worse for plate elements. 1) The curved geometry will be a lot more complex to enter. 2) You may have to use Triangular elements (which are less accurate) because the geometry may mean that a quad plate would be non-coplanar (which is no allowed with RISA's plate element formulation).

 

[dold]

@JoshPlum,
I suppose one could use the high level generation in RISA (circular disk with plates or even part of a geodesic dome) and then adjust elevations of each concentric ring of nodes to start an approximation of this. But i'd imagine you'd run into the non-coplanar issues. I'd have to play with it.

@OP,
STAAD has some non-linear analysis functionality (for cables, at least). I haven't used it though. Just in case you have STAAD.

 

[r13]

The thin plate has load applied to its perpendicular face.

Which face is "its perpendicular face", the plate face (transverse load), or the thickness (axial load)? For a flat thin plate subjects to surface load (pressure) isn't the same as a thin walled pressure vessel that resists the load by tension only. A flat plate will deflect between supports resulting in moment due to piecewise connectivity (rigid joints). Show a full picture of your model with load indicated will help us understand your problem better.

 

[klaus.]

depends on what kind of elements you are using....

 

[canwesteng]

STAAD won't do non-linear on plates, unless it's been added lately.

 

[rb1957]

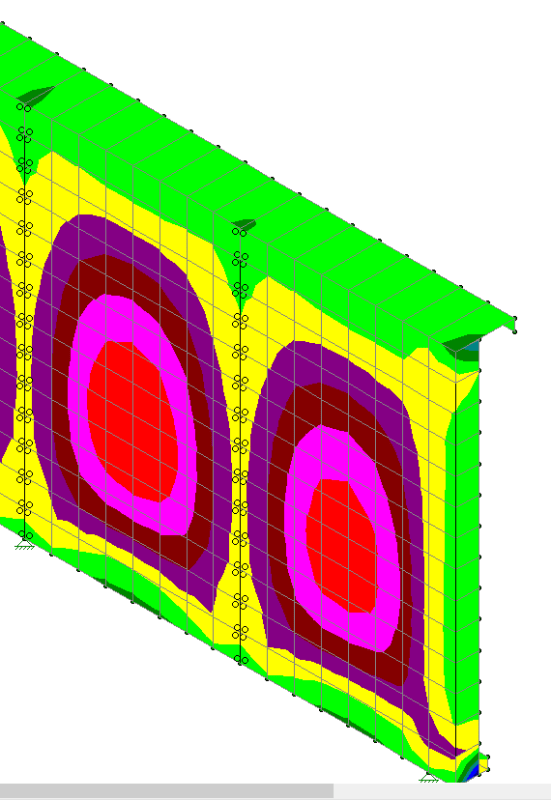
why is (apparently) out-of-plane loading described as "tension" ?

This is a flat panel loaded with pressure. Any/Every linear FEM will tell you this panel will explode, 'cause what's happening is the flat web is deflecting (large displacement) and reacting the pressure as in-plane membrane stress.

Now that I write that, maybe you already know this and were really asking "how do I get a FEM to react pressure this way (as in-plane tension)?" The answer is large displacements, geometry non-linear, maybe hyper-plastic. The alternative is to hand calc it … assume a deformed shape (say spherical, as though the panel has dished) calculate the in-plane stress (hoop stress) that results, compare the strain this creates with the strain in your assumed shape and iterate. You might try Timoshenko, he may have something to say about thin plates. You could try Roark, he's usually got something to say about just about anything and everything.

another day in paradise, or is paradise one day closer ?

 

[r13]

Unless the panel is made of membrane-alike material, bending stress is there.

 

[rb1957]

agreed, there is always some amount of bending just as there is always (in reality) some amount on in-plane tension. In the analysis world, we (ok, I) simplify things to either pure bending (as a plate) or pure tension (as a membrane).

another day in paradise, or is paradise one day closer ?

 

[kphillips]

rb1957 - We agree with your comment that reality would assume there is some amount of bending but from an analysis standpoint we would like to simplify it to pure tension. Because our panel is very thin (0.0747") we know that it really has no bending capacity and would act more like a membrane. We are having difficulty properly analyzing that whether it be in RISA or hand calcs.

 

[r13]

kphillips,

See klaus' comment made on 1 Apr 20 07:58.

 

[Geoff13]

We are having difficulty properly analyzing that whether it be in RISA or hand calcs.

You should know that JoshPlumSE used to work for RISA, and so you should read his comments above carefully, particularly the first line. He helped me understand RISA many times when I contacted support for help.

 

[jjl317]

While it is unclear what this application really is, years ago I spent time trying to refine an approach for analysis of relatively thin architectural panels (aluminum or ACM, up to 1/8" thick), to take advantage of tension / membrane stresses. From memory, I did not have access to an analysis program that could handle non-linear, and I believe the results we ended up with were based on Roarks' formulae for flat plates, without determining a good way to fully include any benefit from tension / membrane (in part due to in-plane forces developed at the perimeter, required to develop the membrane stresses).

I did find an old textbook that you might find helpful (if you can find it) - Thin Plate Design for Transverse Loading - B. Aalami & D.G. Williams - 1975 - good news might be that it is so old it was written before the non-linear analysis was available, and could be used to develop your own analysis techniques.

Hope this helps

 

[rb1957]

From what I've heard, I'm glad I don't use RISA. Is there an issue with following the several hand calc methods proposed ? jjl317 is right, that the imposed in-plane forces (the hoop stresses of the dished web reacting the applied pressure) become the next problem to deal with … bending the edge members.

another day in paradise, or is paradise one day closer ?