Hi All,
Hoping someone might be able to help me with this problem I've been given.
There is a scour valve (150mm diameter) located in the middle of two sections of DN560 PE Pipe. These two sections have a length of 1000m and a slope of 1:100.
In this example I am treating this network as full and separate from any other network. I am assuming the pipe section ends and the valve opening are exposed to the atmosphere thus pressure difference is zero.
The time required to drain the two sections of pipe through the scour valve must be calculated
I've had some trouble finding the correct equations and methods for this problem. I've tried methods using Hazen-Williams equations, I've also using also adapted Bernoulli equation examples that relate to draining a reservoir and relating the change in height(elevation head) to the change in time. This was difficult as the change in the elevation of the water surface was function of the pipe's length and slope.
I've calculated a wide range of answers from hours down 15min.
Looking for some guidance on the correct methods and reasonable assumptions.
Let me know if anyone needs any more information.
Tom
Hoping someone might be able to help me with this problem I've been given.
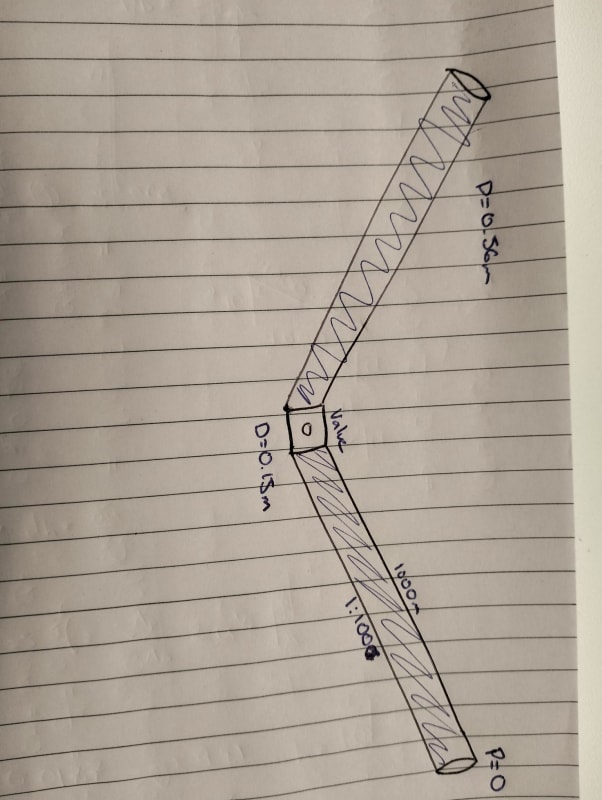
There is a scour valve (150mm diameter) located in the middle of two sections of DN560 PE Pipe. These two sections have a length of 1000m and a slope of 1:100.
In this example I am treating this network as full and separate from any other network. I am assuming the pipe section ends and the valve opening are exposed to the atmosphere thus pressure difference is zero.
The time required to drain the two sections of pipe through the scour valve must be calculated
I've had some trouble finding the correct equations and methods for this problem. I've tried methods using Hazen-Williams equations, I've also using also adapted Bernoulli equation examples that relate to draining a reservoir and relating the change in height(elevation head) to the change in time. This was difficult as the change in the elevation of the water surface was function of the pipe's length and slope.
I've calculated a wide range of answers from hours down 15min.
Looking for some guidance on the correct methods and reasonable assumptions.
Let me know if anyone needs any more information.
Tom


