Nashanas
Petroleum
- Apr 23, 2021
- 54
Hello,
I need help to understand how to select a hydraulic motor to move a structure. Imagine a hinged beam with two concentrated loads on ends. The hinge is not in the center. The gravity is in negative Y direction. And the beam is stable in the XY plane, so the loads and moments are balanced. Now in the XZ plane, I want to rotate the beam about the hinge. How much torque would be required to do that?
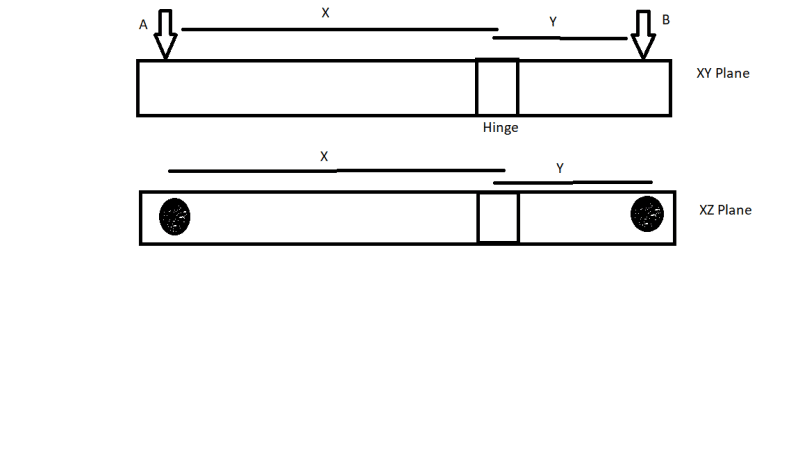
I need help to understand how to select a hydraulic motor to move a structure. Imagine a hinged beam with two concentrated loads on ends. The hinge is not in the center. The gravity is in negative Y direction. And the beam is stable in the XY plane, so the loads and moments are balanced. Now in the XZ plane, I want to rotate the beam about the hinge. How much torque would be required to do that?

