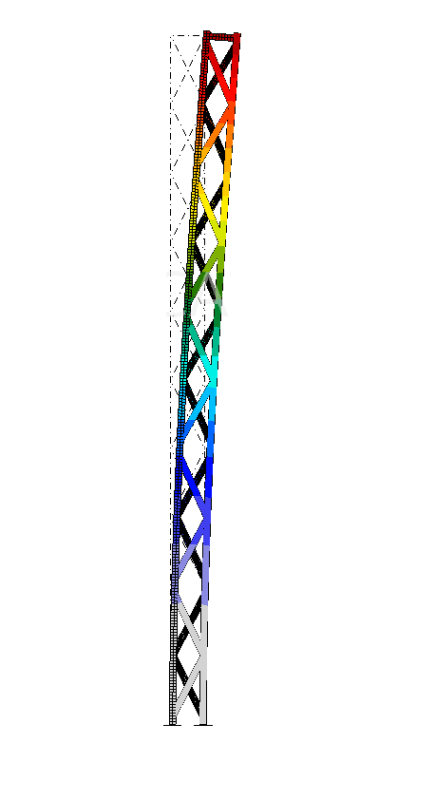Torsion on truss Mutually opposed lacing system 2

[Italo01]

Hello,

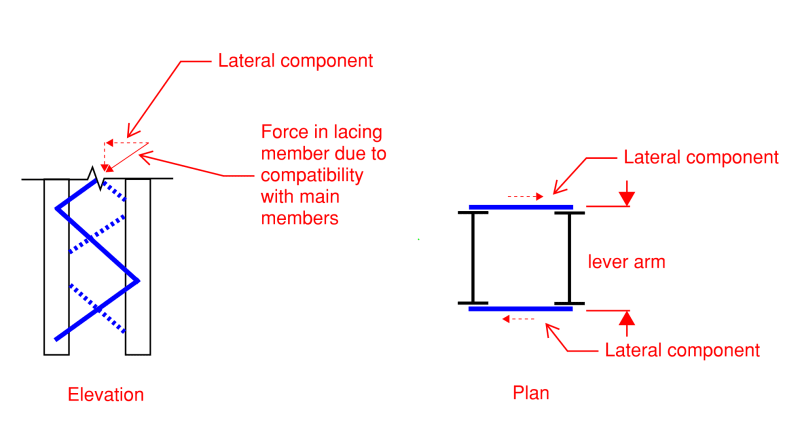
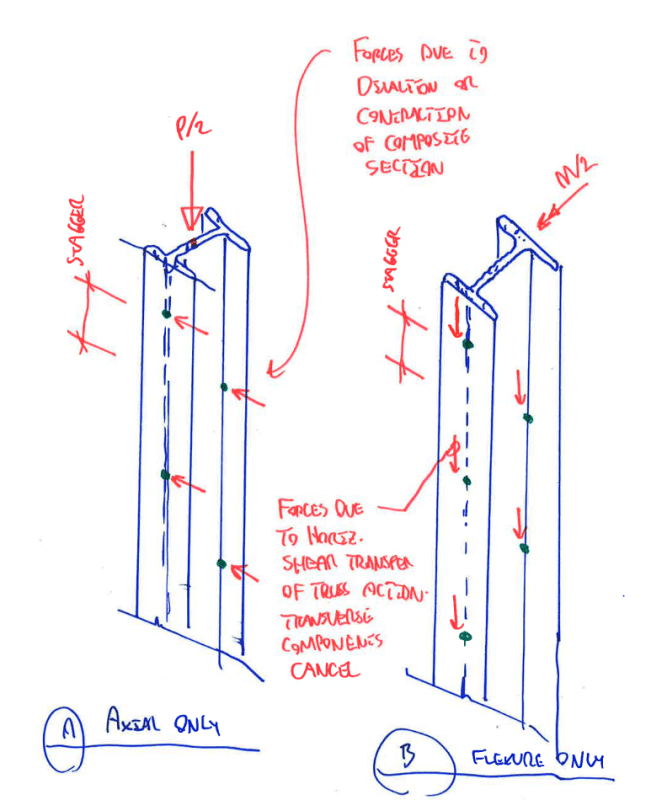
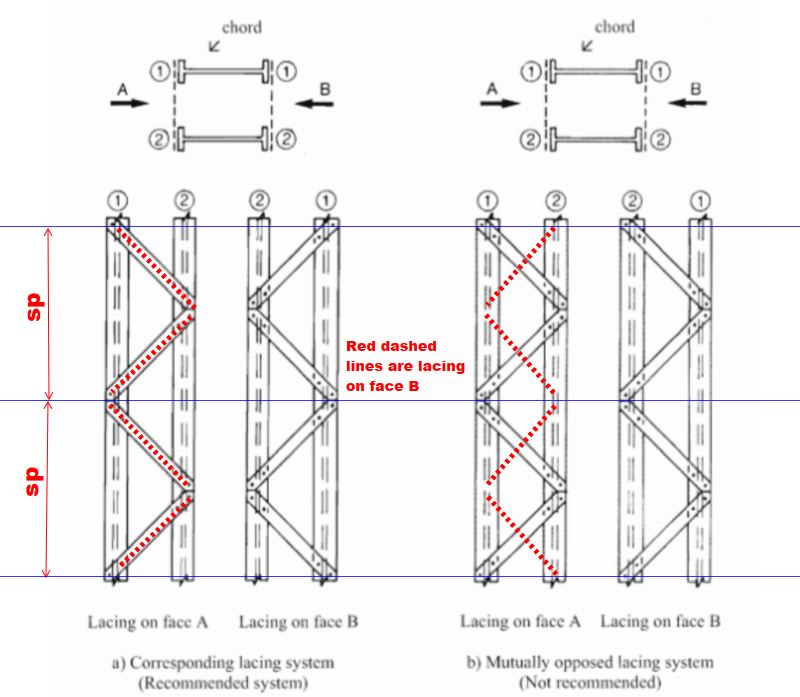
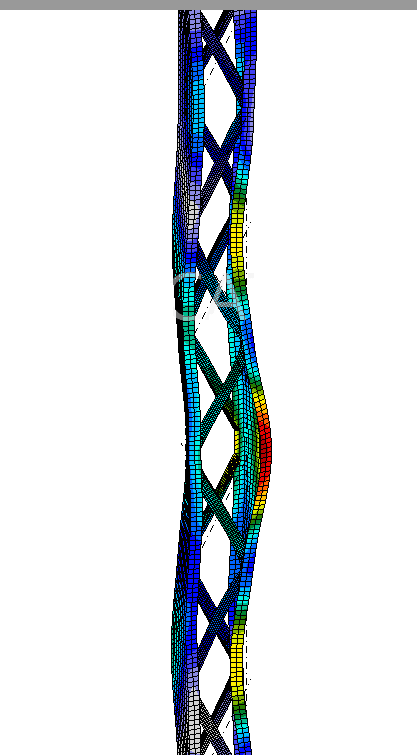
Studying Eurocode 1993 1-1, i've found, in topic 6.4.2.2 (Constructional details), the recommendation about the orientation of the lacing planes on built-up columns shown below.

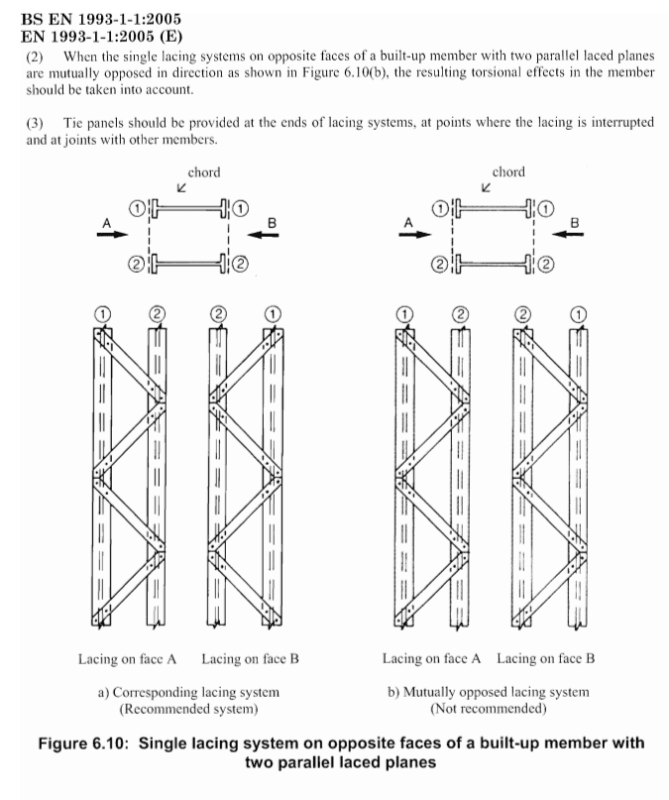
I've never used this mutually opposed lacing system but i see it in my region with a reasonable frequency and i think nobody consider the torsional effects. I'm planning to do some research on this topic and maybe write a paper about it if i verify that the reduction on member strength due to this torsional effects is too great and if there's no paper already written on the subject. Is anyone aware of such paper or has analyzed a structure of such type?

If Eurocode brings a recommendation about it and says that there are torsional effects, i think that someone has done research on the topic but i couldn't find it. Also, Would you suggest a frame analysis with the diagonal ends offset or a complete FEM analysis.

Thank you in advance.

 

[Italo01]

Someone?

 

[MotorCity]

Loading looks symmetrical about the center of gravity. Not seeing torsion.

 

[Italo01]

I interpreted that when the built-up column(or a truss with this configuration) is subjected to bending, one of the diagonals will be subjected to tension and the other one to compression, and since they are not on the same plane, there will be torsion.

Am i interpreting this wrong?

 

[bugbus]

Under axial load or bending, the lacing members will carry some of the compression/tension due to compatibility with the main members.

Under pure compression or tension, if the lacing members are mutually opposed, then the transverse component of the lacing members act in opposite directions (b), giving torsion shown below.

Under pure bending, I imagine you would get the same torsion effect when you have the corresponding lacing configuration (a).

To work out the force carried by the lacing members, either check it with a frame model or I would also recommend looking at Figure 3.7 in Design Guidelines For Steel Trapezoidal Box Girder Systems, which you should be able to find online easily. Those equations are set up to determine the design loads in trough girder bracing members under bending, but it should also apply to your case. I'm sure there are probably many other design guides out there which would tell you how to calculate the compatibility forces in the lacing.

To answer the second part of your question about modelling, I would think a simple frame model with offsets would be enough. Also I would probably just treat the lacing as pure truss members.

 

[HTURKAK]

I visualize ,Your interpretation is OK for the built -up column subjected to horizontal force. In case of pure axial loading , consider the buckling mode together with imperfection.

My points ;

- The clause 6.4.2.2 (2) ( When the single lacing systems on opposite faces of a built-up member with two parallel laced planes
are mutually opposed in direction as shown in Figure 6.10(b), the resulting torsional effects in the member
should be taken into account). This is requirement for analyzing the built -up columns with proposed approximate method at the standard.

- In case of Mutually opposed lacing system, FEM is the way ,

- I do remember a few case only for the use of built -up column with lacing for crane supporting column with heavy loads

- I do not see any advantage for the use of Mutually opposed lacing system superior to Corresponding lacing system. Just use Corresponding lacing system and follow the proposed simple method ..






Not to know is bad;
not to wish to know is worse.

NIGERIAN PROVERB

 

[Italo01]

Thanks Bugbus for the recommendation, i'll check it.

HTURKAK, i don't see any advantage also. The reason i intend to write the paper is to show that this system is always worst, if these are the results of the research, which i think it is. As i said, i see some being used in my region.

 

[KootK]

I'm with MotorCity on this one. I, also, am not seeing torsion in any meaningful sense. See the sketches below where I've considered axial and bending loads independently.

At worst, I see the torsion effect just being a local, come and go effect in the wide flanges owing to the staggered delivery of the forces imposed by the lacing. Under axial, that's torsion. Under flexure, that's a bit of strong axis bending.

My gut feel is that, if you explore this in detail, you'll find that Eurocode recommendation is a "nice to have" but, otherwise, not a very big deal. Given that there is obviously some team disagreement on this, perhaps that alone justifies the exercise of exploring this a bit.

Also, Would you suggest a frame analysis with the diagonal ends offset or a complete FEM analysis.

For me, it would be 3D FEM all the way. But that reflects my particular position on this which is:

1) I don't feel especially confident that I understand the behavior in its entirety.

2) If I am missing something, I would expect it to take a 3D model to show me just what that is.

Obviously, if you're going to write a paper on this and put it out into the world, you want to be sure that you understand the behavior correctly.

I would also expect the magnitude of the dilation/contraction effect to be limited by:

1) The high axial stiffness of the wide flanges which should shield them from this effect somewhat and;

2) The low lateral stiffness of the wide flanges which should prevent them from absorbing much load from this effect.

 

[KootK]

[M/2] should have just been [M] which then imposes a longitudinal forces on the wide flanges as [M/spacing]. You know... statics and such.

 

[BAretired]

The main purpose of lacing bars is to ensure that the local slenderness ratio is less than or equal to the overall slenderness ratio. The overall slenderness ratio H/R where H is the height and R is the radius of gyration of the combined section. The local slenderness ratio of the recommended arrangement in (a) is sp/r where sp is the spacing and r is (I[sub]y[/sub]/A)[sup]0.5[/sup] of one main member.

In the sketch below, members 1 and 2 of (a) are braced to a braced point of each other, whereas they are both braced to an unbraced point in sketch (b). The local slenderness ratio in sketch (b) is not readily obtained, but it must be greater than sp.

I agree that torsion is also a factor, but to me, the above argument is more compelling.

 

[KootK]

The main purpose of lacing bars is to ensure that the local slenderness ratio is less than or equal to the overall slenderness ratio.

I agree and, in that respect, one might argue that the opposed configuration does a better job of bracing the wide flanges because it shortens the distance between weak axis brace points (if one ignores the eccentricity effects). While I wouldn't detail a new build this way myself, I suspect that it might be why OP is seeing the opposed configuration in the wild. I'm guessing that it's a well intentioned means of trying to improve the bracing effect of the lacing.

 

[Italo01]

Thanks Kootk and BARetired for your help. I see that the behaviour is really complex so i'll follow the path of FEA that Kootk recommended.

At worst, I see the torsion effect just being a local, come and go effect in the wide flanges owing to the staggered delivery of the forces imposed by the lacing.

Yeah, I noticed that but maybe even this local torsion may be detrimental to the chord, especially for very thin cold-formed channels, since they have very low torsional strength and stiffness.

The local slenderness ratio in sketch (b) is not readily obtained, but it must be greater than sp.

Very good observation. Maybe the slenderness ratio will be halved for minor axis buckling but will be increased for Torsional buckling. What do you think?

 

[BAretired]

It may be well intentioned, but it increases the effective spacing of lateral support for both main vertical members. I agree with the British code which recommends, in effect, that the lacing members should be mirror images, not opposed.

 

[BAretired]

Under pure compression or tension, if the lacing members are mutually opposed, then the transverse component of the lacing members act in opposite directions (b), giving torsion shown below.

That may be true at the top and bottom of the column where there is a rigid plate preventing the main members from separating, but under pure compression, lacing members remote from the gusset plates will not be stressed at all. The main vertical members will simply separate, leaving the lacing unstressed by the column load.

Similarly, column bending produces no stress in lacing bars. The only applied load which contributes significantly to lacing bar stress is column shear perpendicular to the major axis of each main member. Lacing bars are required to prevent buckling of each main member but the stress required to satisfy that requirement is minor.

A column with high shear applied at the top, in a direction parallel to Faces a or b, using the mutually opposed lacing system, would be subject to torsional deformation, but torsional buckling, in the words of Sherlock Holmes is a two pipe problem.

 

[BAretired]

Maybe the slenderness ratio will be halved for minor axis buckling but will be increased for Torsional buckling. What do you think?

I don't believe slenderness ratio will be halved for minor axis buckling by using the recommended system, but it will be improved.

As for torsional buckling, I don't believe slenderness ratio of members 1 and 2 is an accurate measure, but it is not a simple problem.

 

[MotorCity]

I tend to view this arrangement as a tube like structure that will actually resist torsion quite well. I suspect any local torsion induced by the lacing will be quite small and dissipate before it generates any noticeable twist. Call it "fake torsion". Only FEA will tell.

 

[Italo01]

Hello guys,

I was very busy these past weeks and was not able to do the analysis about this problem, but this week i did it(Linear Buckling Analysis) and found some interesting results.

I analyzed one Cantilevered built-up column but i intend to do a parametric analysis to better understand the system. What i found from this analysis was that:

1 - The flexural buckling failure of the column was not affected by the way in which the diagonals were arranged.

2 - The column is subjected to a torsional buckling mode and for the mutually opposed lacing system, this load is smaller( About 15%) than for the parallel system. When i say Torsion, i'm referring to torsion of the combined section and not torsion of a chord. This mode of failure consists of both chords bending on opposite directions.

3 - The buckling load of the chord for the Mutually opposed lacing system was improved(About 15%), for this particular case, and consisted of a flexural-torsional buckling mode. This confirms what BARetired and Kootk talked about. If the failure mode is chord buckling on the weak-axis, the not recommended system may be better, but its difficult to determine this load.

 

[BAretired]

Interesting, Italo01. Did you consider the lacing members to be pin connected or rigidly connected to the main members?

 

[Italo01]

The lacing members have oneleg welded to the chords, so i consider that in plane they are rigidly connected but out of plane they are pin connected.

 

[Lomarandil]

Thanks for the follow up Italo! Much appreciated.

If you have the time and interest, I'd be curious to see if the results are affected by pin-connection in plane (e.g bolts/rivets).