anewbieengineer
Structural
- Apr 3, 2012
- 10
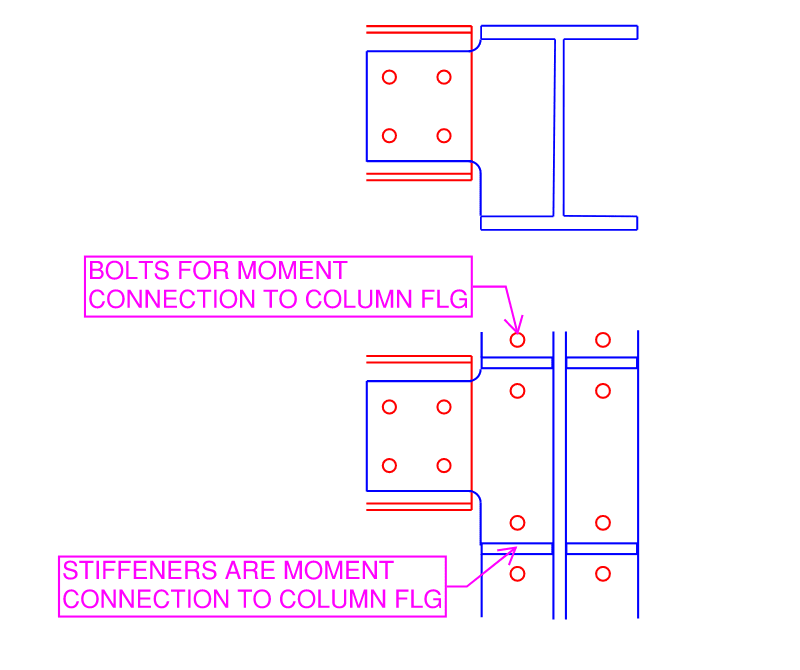
Hi All, I am practicing in Canada but very often we refer to AISC manual for information not available in CISC. I am trying to work on an extended shear tab tool (please refer to attached picture above) and am trying to make it to cover as many different scenarios as possible. I like to use shear tabs whenever possible because it is both economical for fabrication and erection. However, design method provided by AISC is only applicable for beams that are laterally supported, which is common for building with slab and deck, but for heavy industrial projects, infill beams and stringers are often not laterally supported. I was doing a bit of research and came across an example in the text book, "Handbook of Structural Steel Connection Design and Details," Sec Ed. by Akbar R. Tamboli. Under section 2.4.6, he presented a check based on the Australian code for torsional stiffness of extended shear tab (please see second picture attached).

However, he did not provide a clear reference to the origin of the equation. My company is not interested in purchasing an Australia code and I was not able to find further info online. Anyone can shine some light on me. Thanks!!!
