Tek-Tips is the largest IT community on the Internet today!
Members share and learn making Tek-Tips Forums the best source of peer-reviewed technical information on the Internet!
-
Congratulations MintJulep on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
Tourist submersible visiting the Titanic is missing Part 2 69
- Thread starter GregLocock
- Start date
- Status
I agree there are likely only two rings (one at each end). See this pic:
The FEA guy may have made a mistake with the ring geometry. Look at the ring vs the FEA model. The ring proportions seem different in the FEA, as though the FEA ring is twice as long as the real one? Dunno.. it's weird
The FEA guy may have made a mistake with the ring geometry. Look at the ring vs the FEA model. The ring proportions seem different in the FEA, as though the FEA ring is twice as long as the real one? Dunno.. it's weird
Spinney, there is still a difference between our calculations. My velocity is now 3.28 x yours.
I was thinking that it would be an energy/unit mass equality, but it is equal only as far as pressure on a ft2 or a m2. When pressure is equivalent per unit area, Volume, and hence the mass of water we accelerate, differs by a factor of 3.28. We have to decide on a finite mass of water to accelerate. Not sure how we should do that exactly, but it cannot be more than the wedge segment of the tubes cross sectional area described by the radii of the unit area to the tubes central axis. 1 ft3 implies a layer of water 1ft thick wedge moves from the outer shell to the center. 1m3 implies a 1m thick wedge. As the radaii is only 1.5 something, a 1m3 volume appears to be too large. I think we have to do the simulation accelerating many thin layers of water each moving towards the tube axis. That's beyond my pay grade, so I could just agree that it is somewhere inbetween 1/1000 of my original 200ms and whatever your time is, Or we both could just say ... about as instantaneous as you can get. In which case the FEA model may have accounted for water mass accelerations.
--Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."
I was thinking that it would be an energy/unit mass equality, but it is equal only as far as pressure on a ft2 or a m2. When pressure is equivalent per unit area, Volume, and hence the mass of water we accelerate, differs by a factor of 3.28. We have to decide on a finite mass of water to accelerate. Not sure how we should do that exactly, but it cannot be more than the wedge segment of the tubes cross sectional area described by the radii of the unit area to the tubes central axis. 1 ft3 implies a layer of water 1ft thick wedge moves from the outer shell to the center. 1m3 implies a 1m thick wedge. As the radaii is only 1.5 something, a 1m3 volume appears to be too large. I think we have to do the simulation accelerating many thin layers of water each moving towards the tube axis. That's beyond my pay grade, so I could just agree that it is somewhere inbetween 1/1000 of my original 200ms and whatever your time is, Or we both could just say ... about as instantaneous as you can get. In which case the FEA model may have accounted for water mass accelerations.
--Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."
In regards to the plastic view port, was this one piece, or two sandwiched together in a mirror orientation? I have seen photos, and a removed video, of the craft having a flat face view port held on by 4 fasteners with no bolted ring. Unsure if that was just a testing or transport piece as it appears to be their original titan retrofit with stuff from Cyclops 1 from some 2021 testing.
Also, did some more digging around in their press releases but don't have the article handy.
With covid-19 restrictions, NASA was shut down and not manufacturing their pressure chamber. OG employed a hazmat team to enter MSFC to retrieve their materials, which were then brought to private contractors and the new pressure vessel built. The earlier article I posted appears to be some jumping the gun press release from OG.
Also, did some more digging around in their press releases but don't have the article handy.
With covid-19 restrictions, NASA was shut down and not manufacturing their pressure chamber. OG employed a hazmat team to enter MSFC to retrieve their materials, which were then brought to private contractors and the new pressure vessel built. The earlier article I posted appears to be some jumping the gun press release from OG.
1503-44 said:
Yep. 3.28 feet in a meter.
My intent was just to put a number on the collapse at the order of magnitude level. This is a weird calculation to try to make, in that the pressure is the same everywhere (or, at least, the difference in pressure over 1 meter is negligible for our purposes) which means as you make your assumed volume to accelerate smaller, pressure does not change, so acceleration rises rapidly to compensate.
The real value is hard to know without much more detailed math, which neither of us are going to do (at least, I'm not... juice not worth the squeeze, etc). I do think that a thinner layer makes more sense - if I had a gun to my head, I'd bet your updated number may very well be closer to reality than mine.
But ultimately, I think if we're talking within the same order of magnitude (which we now are), we're close enough for our purposes.
- Moderator
- #86
I'm having trouble accepting the acceleration of a volume of water, such as 1 cubic foot or other volume.
When that cubic foot accelerates, it doesn't leave behind a vacuum.
An expanding cone of water behind the subject cubic foot also accelerates, at a reduced rate, depending on the distance from the breach.
The expanding gas bubble may also be misleading.
As the bubble of air in the hull is compressed to 400 atmospheres, it will be at equilibrium at about 1/400 or 0.25% of the original volume.
If inertia takes that down to a smaller volume, the rebound volume will still probably be less than 1% of the original volume.
The bubble from an explosion will be many times the volume of the hull, and will be at a pressure above the pressure of the surrounding water.
The ratio between the bubble volume of even a small explosion compared to the bubble volume the implosion will be some multiple of 400:1.
I suspect a progressive failure and collapse of the hull in such a way as to tear the composite away from the end rings.
I suspect that the recovered titanium parts may have been brought the last few feet to the surface on the launch platform, and that the ring bolts and possibly the viewport bolts were removed there in order to make a safe lift onto the deck of the recovery vessel.
I am waiting to see, and I won't argue this suggestion strongly.
--------------------
Ohm's law
Not just a good idea;
It's the LAW!
When that cubic foot accelerates, it doesn't leave behind a vacuum.
An expanding cone of water behind the subject cubic foot also accelerates, at a reduced rate, depending on the distance from the breach.
The expanding gas bubble may also be misleading.
As the bubble of air in the hull is compressed to 400 atmospheres, it will be at equilibrium at about 1/400 or 0.25% of the original volume.
If inertia takes that down to a smaller volume, the rebound volume will still probably be less than 1% of the original volume.
The bubble from an explosion will be many times the volume of the hull, and will be at a pressure above the pressure of the surrounding water.
The ratio between the bubble volume of even a small explosion compared to the bubble volume the implosion will be some multiple of 400:1.
I suspect a progressive failure and collapse of the hull in such a way as to tear the composite away from the end rings.
I suspect that the recovered titanium parts may have been brought the last few feet to the surface on the launch platform, and that the ring bolts and possibly the viewport bolts were removed there in order to make a safe lift onto the deck of the recovery vessel.
I am waiting to see, and I won't argue this suggestion strongly.
--------------------
Ohm's law
Not just a good idea;
It's the LAW!
I thought the FEA model looked a little off.
If there were only two rings, then it's interesting that neither ring was found connected to its corresponding end cap, although, from the photos, the bolts holding them together weren't particularly large.
As for the implosion timeframe, I'd go with the single digits milliseconds after the hull was breached. If we consider one inch area (5 inch deep) of CF accelerated by the hull pressure, we get
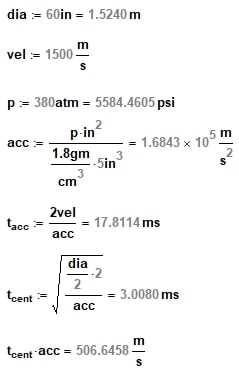
So, it takes only about 18 ms to accelerate to the speed of sound in water at that depth, and only about 3 ms to even reach the center of the hull, ignoring any resistance the hull might have provided and the water density changing. 3.5 ms is long enough for the water to fill in behind the CF chunks. We could argue that this might drop the apparent pressure, but halving the pressure only changes the number to 4.3 ms, so whatever exactly happened, it occurred within a few milliseconds.
TTFN (ta ta for now)
I can do absolutely anything. I'm an expert! faq731-376 forum1529 Entire Forum list
If there were only two rings, then it's interesting that neither ring was found connected to its corresponding end cap, although, from the photos, the bolts holding them together weren't particularly large.
As for the implosion timeframe, I'd go with the single digits milliseconds after the hull was breached. If we consider one inch area (5 inch deep) of CF accelerated by the hull pressure, we get
So, it takes only about 18 ms to accelerate to the speed of sound in water at that depth, and only about 3 ms to even reach the center of the hull, ignoring any resistance the hull might have provided and the water density changing. 3.5 ms is long enough for the water to fill in behind the CF chunks. We could argue that this might drop the apparent pressure, but halving the pressure only changes the number to 4.3 ms, so whatever exactly happened, it occurred within a few milliseconds.
TTFN (ta ta for now)
I can do absolutely anything. I'm an expert! faq731-376 forum1529 Entire Forum list
The layer of water behind the initial layer has exactly as much pressure forcing it inward as did/ does the initial layer, but now no liquid in front of it "holds it back". Its following the first layer in with the same acceleration as the first and just as quickly as the first, a chain of railroad cars linked together, no springs in the couplings. The second layer immediately follows the first. Any air is immediately adsorbed into the water at that pressure. All that would probably happen faster than a pressure wave can be transmitted in water, and like a black hole, no energy could escape, so all goes in the one direction towards the center. Above critical velocity, waves do not travel upstream. At impact, only then is it nearly all reflected outward, a void (of water vapor at its vapor pressure) is probably created again, and I'm neglecting any temperature changes, a HUGE error, as we will see). The size of the void continues to expand, until the power flux decreases with the expanding surface area of the spherical pressure wave until further outwad expansion cannot be sustained, overcome by wthe cumulative effect of water's high bulk modulus, which reverses the action to implode once again. Like the pulsed diagram of the process of an atomic bomb shown somewhere up above, each wave reducing in power until it finally is dissipated. Cavitation is much the same process, which is why it can be so destructive. There are actually some shrimp that kill their prey by snapping their claws so fast that the resulting shock wave from cavitation that was created kills or disables their immenent meal.
The Pistol shrimp, temperatures as high as the surface of the sun
--Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."
The Pistol shrimp, temperatures as high as the surface of the sun
--Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."
LittleInch
Petroleum
The bolts holding this thing together for both the end cap and the viewport were only there to stop the end caps and view port from falling off when this thing was on the vessel and to stop water getting in from wave action / right on the surface.
As soon as this thing descended more than 5-10m, the external force from the sea became the sealing force.
When you look at the size of the components and the size of the bolts they would be unable to hold more than about 1 bar internal pressure IMHO or maybe 10 at the very most. The extraordinary violent implosion would have sheared them all virtually instantly.
Remember - More details = better answers
Also: If you get a response it's polite to respond to it.
As soon as this thing descended more than 5-10m, the external force from the sea became the sealing force.
When you look at the size of the components and the size of the bolts they would be unable to hold more than about 1 bar internal pressure IMHO or maybe 10 at the very most. The extraordinary violent implosion would have sheared them all virtually instantly.
Remember - More details = better answers
Also: If you get a response it's polite to respond to it.
waross said:
Correct - but at the depth we're talking about, the amount of energy available to feed the collapse - basically 100% of the potential energy of the water column above the sub - is hundreds or thousands of times larger than the amount of energy it takes to accelerate the volume of water required to close the bubble. In simplest terms, you're talking about a reservoir of potential energy 3800m tall, which only 'falls' 1.5-2m. There's a large amount of energy consumed in the collapse, but that large amount of energy is still a tiny percentage of the energy available.
Point is, yes- there's energy required to 'backfill' the volume of the collapsing hull - but the energy required is coming from an infinite reservoir.
waross said:
It would be at standard temperature and pressure. But we aren't talking about standard temperature and pressure - we're talking about a 6000 psi environment.
When an explosion happens underwater, the explosive becomes a cloud of gas, rapidly expanding. At some point, assuming the explosion is deep enough to not breach the surface, the expanding gas bubble reaches a point where the gas pressure and surrounding water pressure are equalized, at which point the gas bubble stops expanding and the water causes it to collapse. When the bubble collapses, effectively all that water slams together at the center point of the explosion, creating an extremely powerful shock wave.
This collapse would have involved the same interaction - surrounding water accelerating to fill the void at extremely high speed. Imagine a scenario where instead of imploding, we stopped time and just waved our magic wand and caused the sub to cease to exist, leaving behind a Cyclops II shaped hole in the water, filled with air, at 3800m. If that bubble of air was preserved and allowed to float to the surface, its volume would expand by your 400x multiplier.
If you make the analogy to an explosion, the upper limit of the energy involved in the collapse of the sub is exactly the same as the explosive energy it would take to create a gas bubble of the exact same volume as the sub, at 6000 psi ambient pressure.
Alternatively, the energy involved in the explosion would be the amount of explosive energy required to create a gas bubble 400 times the volume of the pressure hull at standard pressure.
We can actually calc this out. On average, TNT produces roughly 1 liter of gas at standard pressure, per gram. The approximate volume of the hull of the sub is/was 8.1m3
8.1m3 = 8100L
8100L gas = 8100g TNT at standard pressure, or 8.1kg of TNT.
If you assume 400 bar pressure environment for the 'explosion', to create a gas bubble of 8.1m3 volume, you would need 3,240kg of TNT.
That's not a nuclear level of explosive energy.. but 3 tons of TNT is a LOT of energy.
It disappears as it is absorbed by water at high pressure, like CO2 bubbles in a Coca-Cola bottle, most is in solution until the pressure is released. If that block of water makes it to the surface, it will degass.
--Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."
--Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."
Yep. That 8 m3 of O2 was transported down to the bottom of the ocean, never to return to the surface.
That's another component that would add destructive energy. The water at the very front of the pressure wave resulting from failure of the hull would not only be moving extremely quickly - it would also rapidly lose any gasses in suspension.
Probably only a small percentage of the total energy. I also don't know the typical quantity of gas in suspension for water that deep. There must be some, since stuff does live down there.
That's another component that would add destructive energy. The water at the very front of the pressure wave resulting from failure of the hull would not only be moving extremely quickly - it would also rapidly lose any gasses in suspension.
Probably only a small percentage of the total energy. I also don't know the typical quantity of gas in suspension for water that deep. There must be some, since stuff does live down there.
waross said:
It will if it has to. Look at the Hydraulic Press video mini test implosion, where are large vacuum bubble appears outside of the hull, due to the water going into the hull. This was at 80 bars.
The implosion was far more violent than you're imagining it.
That's the cavitation void.
On an aside note, GPT CHAT WARNING
maybe this deserves a thread all on its own. Yes. I will do that.
Basic physics question.
--Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."
On an aside note, GPT CHAT WARNING
maybe this deserves a thread all on its own. Yes. I will do that.
Basic physics question.
--Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."
- Moderator
- #99
If its Lbs-force then Lbs-force x distance is a unit of potential energy.
Power is energy/unit time. i.e. ft-lbf/s i.e. 1 Horsepower = 550 ft-lbf/s
Well, that is what makes the hydro turbines go round and round.
-Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."
Power is energy/unit time. i.e. ft-lbf/s i.e. 1 Horsepower = 550 ft-lbf/s
Well, that is what makes the hydro turbines go round and round.
-Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."
- Status
Similar threads
- Locked
- News
- Question