Trying to find geometric parameters from the volume fraction (0.2), not sure if I have done it right

[tugni925]

I am trying to find the relation between geometric parameter "a" and "b" using that the volume fraction is 0.2.


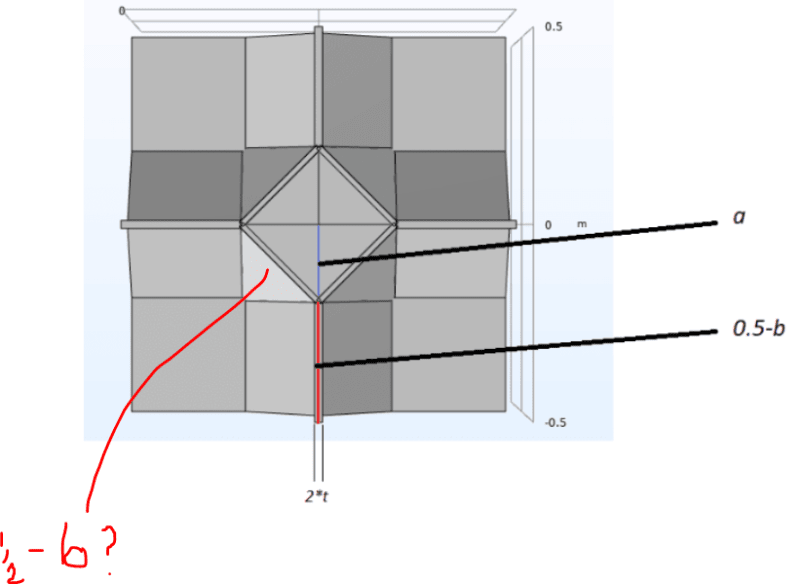
Fig 1: This is the geometry I am working with, its symmetric about xyz axis so I divide it into 8 similar parts:

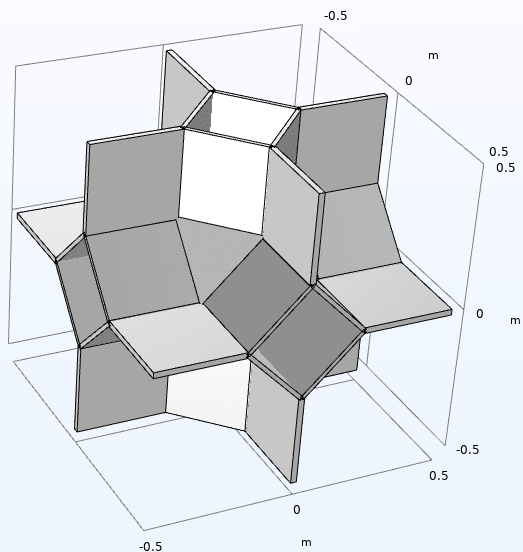
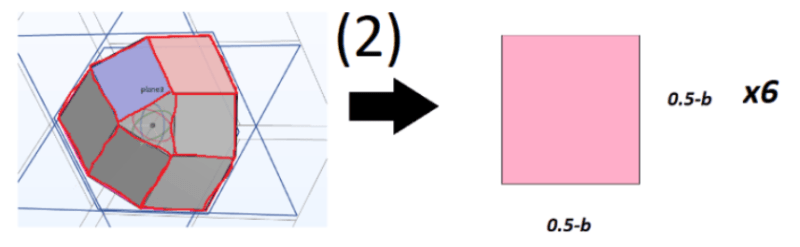
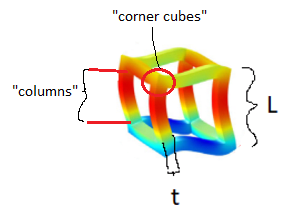
Fig 2: Looking at 1/8th of the geometry - I want to find the volume of this part which consists of:

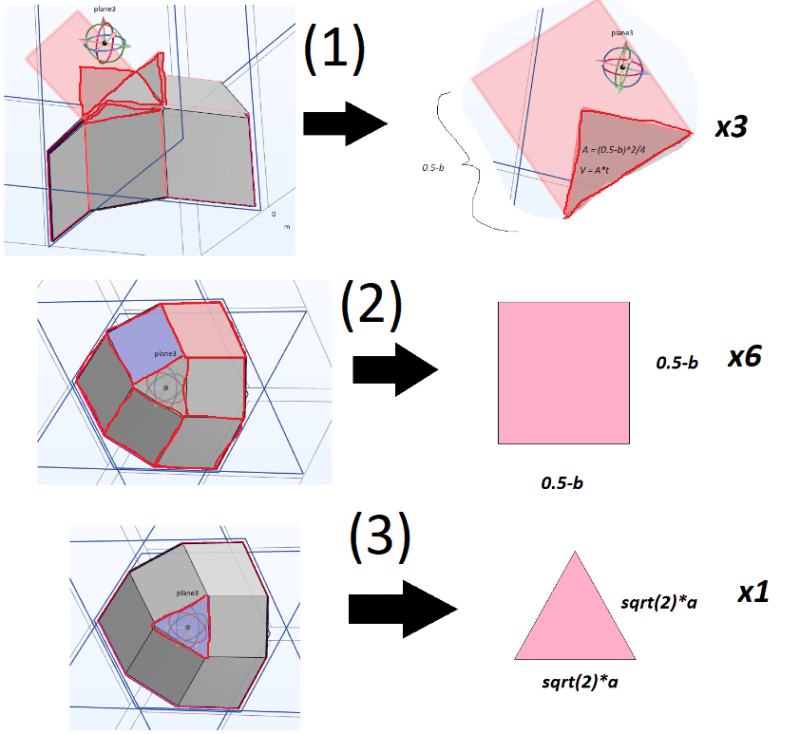
x3 triangles with thickness t (1),

x6 rectangles with either thickness t or t/2 (2)

x1 triangle with thickness t (3)

I calculate the volume of these parts, add them together and it comes out to be:

5.25*t*(0.5-b)^2 + sqrt(3)*a^2*t/2


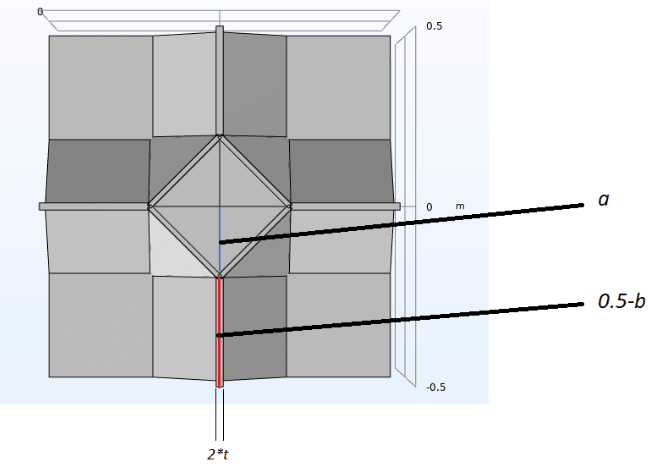
The volume of the 1/8th part would be (a+0.5-b)^3 if it was a regular cube:

So the volume fraction would be given as:

[5.25*t*(0.5-b)^2 + sqrt(3)*a^2*t/2]/[(a+0.5-b)^3] = 0.2

My problem with this is that I get 3 parameters; "a", "b" and "t". If I only had "a" and "b" in the equation without "t" for example I could easily find the relation between these two parameters and maybe ended up with something like 0.78*a = b.

Does anyone have suggestions on how I should go about doing this, I am kind of stuck here right now.

 

[rb1957]

I would look at one quadrant of your pattern ...
3 square/rectangular faces with t/2,
3 square/rectangular faces with t,
1 triangular face with t.

Are you getting hung up on the (tiny) area overlap between the faces ?

How about calculating the volume of the voids ?
there a small triangular pyramid on the "inside corner" of the quadrant,
there a 3 simple cubes/rectangular prisms (on the square/rectangular faces),
there are 3 triangular prisms on each inclined face,
and 1 triangular pyramid on the "outside corner".

another day in paradise, or is paradise one day closer ?

 

[tugni925]

I dont know, it seems a bit more complicated to me to split it into 4 rather than 8.

Edit: I might try it a bit later if 1/8 does not work out.

 

[IRstuff]

Please refrain from double posting

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm

 

[rb1957]

1 quadrant would be 1/8 of the piece.

the volume of 1/8th piece would be 0.5^3, no?

is "a" the open face dim'n, or the CL?

is the thickness of each web "2t" ? then I'm surprised that you have a "t/2" term

is the length of your red line "0.5-a" ?

another day in paradise, or is paradise one day closer ?

 

[onatirec]

It's not really clear what your end goal is. If you want to parameterize volume fraction using a&b but not t, why not just assume an arbitrary value for t?

If this is going to be built at some point, why not use the most likely (or common) value for t?

For that matter, why not just leave t in the equation - if you don't currently have a value for it??

 

[rb1957]

I thought he solved for thickness to achieve a desired filled volume ratio (20% ?)

another day in paradise, or is paradise one day closer ?

 

[onatirec]

ok. i didn't double check all their math, I was just looking at the question in the OP... but it looks like the eq is overconstrained.

at a glance, it seems a=(1/2 - b)/sqrt(2), no?

just replace "a" with the expression using b above (or vice versa) and you have an equation for two variables, one of which is t.

parameterizing some function a(b) would change the geometry

 

[rb1957]

I think there's a typo (or confusion). The whole 1/2 side is 0.5 long, the two segments from be "a" and "0.5-a"; it could be "b" = 0.5-a.
that diagonal length (you call "1/2-b") would be sqrt(2)*a ... no?

it's possible that the shape is "a" (and 0.5-a) on one side and "b" (and 0.5-b) on the other,
so that the diagonal is sqrt(a^2+b^2) ...
or possibly anything !

another day in paradise, or is paradise one day closer ?

 

[onatirec]

The more I look, the more issues I see... If a is specified, then the measurement "0.5-b" should actually be "0.5-a"...

Either way you slice it, if those are (6) squares, then "a" and "b" have a known relationship...

I'm just looking at the information in their post, specifically this pic in the OP:

otherwise, the area/volume calculation used (0.25 * (0.5-b)^2)) would be wrong, as would the rest of the math.

OP needs to start again at the beginning and more clearly lay out the constraints.

 

[tugni925]

Thanks for the answers guys, I will try to give some context on what I am trying to do by using an easier geometry:

In this model there are only two geometric parameters - "t" and "L".

The volume of this is given as:

"Corner cubes" = t^3*8

Columns in the middle of these corner cubes = t^2*(L-2*t)*12

Total volume comes out to be = t^2*(L-2*t)*12 + t^3*8

If it was just a cube the volume would simply be L^3

Then the volume fraction equation is given as (t^2*(L-2*t)*12 + t^3*8)/L^3 = 0.2

From this I get that t = 0.14357*L. This is useful to me because no matter which value I use for "L", as long as my "t" value is 0.14357*L, the volume fraction will always be 0.2. So when I go back to my model in a years time and want to change my L from say 0.1m to 0.2m the "t" value will adjust automatically so that the volume fraction remains at 0.2 since I havent defined it as a constant but as an equation.

Edit: It seems onatirec solved my problem by using pythagorean theorem and saying a=(1/2 - b)/sqrt(2), I just have to test it. I wanted to automate this process for different kinds of geometries, which I think might be harder than I expected.

 

[rb1957]

are you fussed about the over-laps, or is near enough good enough ?

your cube example was very easy to define without overlaps. With your inclined surfaces, is the face volume the exposed face*t
so "a" is the exposed side ? but then b .NE. 0.5-a

another day in paradise, or is paradise one day closer ?