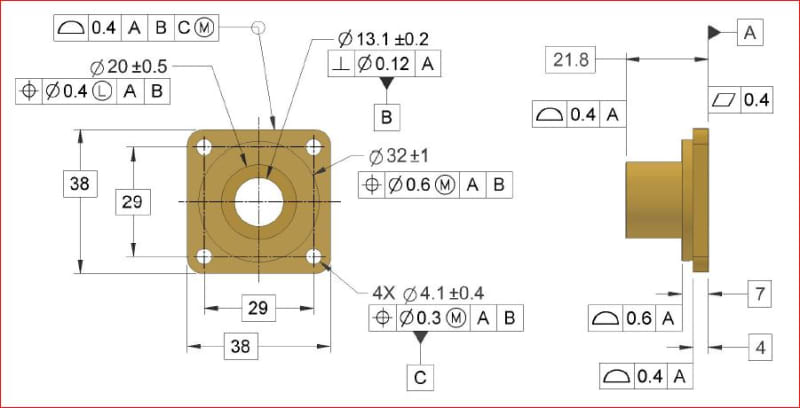
pylfrm 1 May 19 02:17 said:
If the higher-precedence constraint is removed or changed, the interaction between the lower-precedence datum feature simulators and the corresponding datum features will change. This will affect the resulting constraint of [w,x,y].
pylfrm 1 May 19 02:17 said:
The primary and tertiary datum features are both involved in the constraint of [w] because the basic orientation relationship between their simulators must be maintained
Thank you, these were the puzzle pieces that I was missing. I assume we can say that B does not have a basic orientation relationship with C because it does not constrain any rotational DOF because [u,v] is already constrained by A, correct? And if the DRF was instead |B|C>| then B (now primary) would be involved in constraint of [w] as well as [x,y]?
I am trying to put this into one overarching statement - below I have repasted and modified my initial statement. Do you think this is an accurate summary? And if not, maybe what you would change? I feel like theres a better, more precise way of stating the bolded portion about translation modifiers but I'm coming up blank.
[x] cannot be fully constrained "everywhere" until [v,w] is constrained, same with [y] and [z]. Likewise a datum feature that constrains [v] or [w] is also involved in fully constraining [x] (again, rinse/repeat for [y] and [z]).
If [v] or [w] has not already been constrained by a higher order datum feature, datum feature that constrains [x] is also involved in constraining [v] or [w],
unless the location relationship between the datum feature which constrains [x] and the datum feature constraining [v] or [w] is removed by use of the translation modifier and the datum feature constraining [v] or [w] can do so without involving the datum feature which constrains [x]. If a higher order datum feature has an orientation relationship to the datum feature which constrains [v] or [w], the higher order datum feature is involved in constraining [v] or [w] (because the relationship between the datum features and their simulators would change if it were removed). Again repeat with the applicable rotational DOF with [y] and [z].*
Thanks again for your help in grasping your vision of sequential DOF constraint, this has been hugely educational!
*Edit - added that it is repeated with [y] and [z]