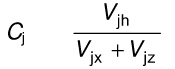What about Biaxial Shear in RC? 1

[Mainu]

Let´s take a rectangular RC column subjected to an action with components along both axes. Here we have the common issue of biaxial bending that we can solve routinely and about what we can find numerous references. But... What happens with shear? How do we deal with the biaxial shear? In this case, references (even in the most reputed books about concrete design) dissapear...

Some people have their own thumb rules. Ones decide to design the reinforcement for Vx and Vy and later add both numbers to obtain the required steel. Other ones think that it is possible and reasonable to design for sqrt([Vx]^2+[Vy]^2) along the main direction. But... Is there nowadays some scientific paper, code, or research to support our designs about this topic?

I would be glad to hear your thoughts about this and, of course, if any of you have some good reference about this topic and he/she wish to share it with the community, it will be highly appreciated.

Thanks in advance.

 

[JAE]

I found this abstract online - applies to columns where you'd typically get more biaxial shear conditions:

https://www.sciencedirect.com/science/article/abs/pii/S0141029616303923

A paper (not ACI/USA):

https://pdfs.semanticscholar.org/e171/552286e21feef14f3b9b00b04cbc3c531f47.pdf

Another paper (attached below)

A previous thread: thread507-18170

Another paper:

https://iopscience.iop.org/article/10.1088/1757-899X/713/1/012029/pdf

There's many more out there from a google search.

ACI 318 doesn't seem to address it at all.

 

[Mainu]

Thank you very much, JAE for your answer. You are the one. (I must admit that I was expecting a little more interaction in this thread. I would like more direct experiences and criteria about this topic. It seems that not many people have doubts when cases not covered by the codes frequently appear... I.e. or nobody here designing columns in seismic zones to resist biaxial shear and with reasonable doubts about the code silence...)

I knew and I read some time ago the other threads in this forum about biaxial shear. And I also knew some of these articles, but I continue the same. I would prefer a contrasted procedure at U.S.

Some comments, about the references that I got access.
*Thamrin´s paper does not deal with shear reinforcement, so it just serve us to understand how the concrete itself works.

*I knew the paper entitled “Behavior Of Rectangular Reinforced Concrete Beams Subjected To Bi-Axial Shear Loading” that deals with the prescription of the japanese code (JSCE). I´ve read it some years ago. But I wonder why we can not find a similar rule in other more familiar codes in U.S. Are there not U.S. researchers in this branch?

*(Right now I got Access to the first link, so I am going to read it with care).

 

[JAE]

To be honest, if I was designing a beam with significant shear in both directions i might take a conservative seat-of-the pants approach.

Determine phiVc based on each direction (each's unique b and d values).
Then only count on a limited percentage of the phiVc in each direction based on the relative magnitudes of the two shear loads coming in and throw an extra safety factor on it - say a 0.75 additional phi.
Then with these reduced, conservative phiVc values separately determine a Vs for each direction and then add the stirrups accordingly.
Note that the pairs of legs of an enclosed stirrup can all be utilized for the separate shear directions (i.e. the horizontal legs used for the sideways shear and the vertical legs for the vertical shear.

I haven't studied the linked articles too close so I'm not positive that my simpleton method indeed is always conservative.

 

[r13]

I've never ran into this type of problem, usually shear in one direction will dominate the design. I agree with the above, a completely enclosed stirrup can work for both directions, similar to the effect on torsional stirrups. Design for each direction then add up would be a conservative approach. I wouldn't use the square root of square method, as the resultant force lies in a skewed angle to the design axes, kind of confusing, isn't it?

 

[BAretired]

With a circular column, there can be no biaxial shear. The resultant shear doesn't care which direction is X or Y. In any direction, the shape is the same.

With a square or rectangular section, perhaps it could be regarded as the shape resisting a resultant shear. That shape is neither square nor rectangular. Looking at it another way, isn't it similar to an odd shaped beam resisting shear. Just a thought.



BA

 

[JAE]

BAretired - that is a good point - for a rectangular column with biaxial shear - it could be looked at as uniaxial shear on an angled axis with a contrived "d" and "b". Still some assumptions and seat-of-the-pants design unless you dive into those methods I linked above.

 

[Agent666]

Beam column joints in a two way frame is one region where my local code NZS3101 is pretty clear, just assess the joint shear capacity (concrete and reinforcement legs) in each direction independently. There is a factor for proportioning the beneficial or detrimental effect of axial load to each orthogonal direction, this might have some merit in looking at member bi-axial shear in two independent directions using the x and y components of 'd' based on the moment actions at that point? i'e d is the position of the resultant reinforcement tension force (not to be confused with the centroid of area of reinforcement in tension).

But I believe this is probably a little different than looking at the shear in both directions some way along a member, but perhaps a starting point for something logical.

I've often thought about this in the past but never found anything in a code that really addresses it. Seems like a hole in how things are supposed to be done. We all understand one way shear in beams and columns, but for a column under bi-axial moment with shears in each direction codes seem to be absent on firm advice.

NZS3101 has this to say on the matter:-

In columns, which intersect with beams on two or more axes, the simultaneous action of the shear forces applied by the beams on each axis should be considered in the design for shear in the column. In such cases the shear resisted by the concrete should be proportioned between the two axes of the column

Doesn't really tell you how, but maybe the clue is in the beam-column joint equation noted earlier:-

The factor Cj is introduced to allocate the effect of axial compression to the two principal horizontal directions x and z of a space frame where a joint is required to transfer joint shears Vjx and Vjz concurrently in each direction. For unidirectional joint loading Cj is unity

You can certainly quite easily assess the efficiency of a bar at an angle to the resultant shear force, but what 'd' to use in the typical d/s ratio for shear capacity? Use 'd' at the angle of the shear based on flexural assessment to work out concrete effective shear area (equivalent of d x b being the area of concrete above the effective depth on the angle), then proportion it to each orthogonal direction using Cj concept. Or better to divide into two orthogonal checks with d_x and d_y values and two effective areas for the concrete component?

 

[Agent666]

Well it seems ACI318-19 now covers some bi-axial interaction for shear. They suggest you look at it independently, but they don't really seem to explain how the concrete/steel contribution is supposed to be calculated.

I'd still guess working out the concrete contribution on the basis of an effective area of concrete being based on a line that is parallel to the neutral axis but located at 'd' depth is the way to go (similar to BAretired suggestion regarding an odd shaped beam). Use the area of concrete above this line towards the extreme compression fibre as the equivalent area = b_w x d. Then proportion the concrete contribution to each direction. Steel contribution worked out normally on orthogonal axes, using the component of the effective depth in that direction. Carry out the interaction check if you hit any of the limits noted.

 

[r13]

Although it wasn't explicitly indicated, I think the bi-shear phenomenon is similar to bi-axial stress/moment in two way slab (Sxy, Mxy. However, for the rectangular beams/columns, unlike the slab resists the twisting force through orthogonal bars, the bi-shear occurs on the same bar at different locations. I believe, design for the larger, or dominate, shear force of the two will satisfy the requirement for both directions.

 

[IDS]

I believe, design for the larger, or dominate, shear force of the two will satisfy the requirement for both directions.

It seems that ACI 318 disagrees, and so do I.

At each stirrup location the shear crack will still intersect the stirrup at two opposite faces, and the bars on the other two faces won't be doing anything. The active bars won't even be parallel to the direction of the shear force. In the case of two equal components on a square section designing for just one of the components would be like dividing the shear force on a circular section by root 2.

Agent666 - do you know if bi-directional shear was a significant cause of failure in the Christchurch earthquake?

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[r13]

No need to agree or not, practice as you feel fit. Until this point, the code is mom on this issue, however, how many structures subjects to bi-moment, thus bi-axial shear at a daily base? When you have lateral load get into a member with weight, there is bi-forces, or tri, to be exact.

 

[IDS]

I'm not sure what your point is. Are you saying the number of problems with shear failures over the years is so small we don't need to worry about it?

If the main US concrete code now says designers should look at the effect of combined biaxial shear, I don't think it's a good idea to recommend a procedure that ignores that.

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[r13]

Until ACI or any code authority can straight faced to tell the engineers what you did was wrong by ignoring such effect, and admit it was ignorant until the finding of the majority of failures are due to this effect, I'll have difficulty to accept the new rule as it is. I don't think it will/can issue such statement, nor admit anything about past shortcoming, but to say "the code has never told you not to take bi-shear into consideration, though not explicitly advocate it, isn't that true? Scary!

I didn't look closely into the code provisions/formula cited above, but in a sense, I thick Vc is more critical under multi-dimensional stresses than steel, which requires more researches, and further change is anticipated. Therefore, advice to the older engineers is don't lose sleep over this; for the younger engineers, follow the code with suspicious mind. Be conservative with reasonable means.

 

[IDS]

I didn't say people should lose sleep over it. I said they should follow the code. That applies to anyone working on real projects, regardless of their age.

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[r13]

Here we agree.

 

[Trenno]

stuff

I sense another Engineers v Sheep blog post on the cards!

 

[Settingsun]

The ACI method is as simple as it looks based on Agent's snippet. I wonder whether the tests were only on squarish sections though.

Update: Umehara and Jirsi tested 300*300mm and 410*230mm columns. 910mm high, so quite stocky. It was related to EQ performance so the stirrups were spaced closely at about 1/5 of effective depth. Seems as though the concrete contribution, which needs to be shared by the two directions, might be a relatively small proportion of the total, compared say with beams that only have minimum shear reo. I haven't read carefully but those are initial thoughts.

 

[Mainu]

…a completely enclosed stirrup can work for both directions, similar to the effect on torsional stirrups. Design for each direction then add up would be a conservative approach.

In fact it can work for both directions. I agree about this point. Indeed this is the way as I work. But in that “would be” is the doubt (at least, my doubt). Is it always a safe procedure? That´s the point for me.

Studies about the effect of biaxial shear are quite limited and they deal with square shapes. So, I think it´s even risky to extract conclusions to rectangular shapes…

I agree with JAE about the “seat-of-the-pants design”… because so little test and research and code silences just reveal our ignorance.
Anyway, for now, we should use what we have… the uniaxial formulation. And here I completely agree when JAE states:

Then with these reduced, conservative phiVc values separately determine a Vs for each direction and then add the stirrups accordingly.

Right the same than when we design for shear and torsion. In such cases you calculate the reinforcement area for each action (shear and torsion), add up them and then choose the proper amount of reinforcement.

Even, in seismic zones, I would consider Vc = 0.

I wouldn't use the square root of square method, as the resultant force lies in a skewed angle to the design axes, kind of confusing, isn't it?

If you talk about design for V = sqrt([Vx]^2+[Vy]^2) along the main direction… yes, I don´t like that method too. But undoubtly that is the real resultant force on the section. And a rigorous method should maybe work with that V.

 

[Mainu]

Wow. I wrote that before reading the new contributions at the thread. I haven´t the new ACI 318-19 (I continue in ACI 318-14) and now I come to see that article at the first time. So I think they are great news.