-
1
- #1
Hello ladies & gents,
I'm tendering on a mechanical plumbing job for this building with the air-cooled chillers & all other equipment located on rooftop.
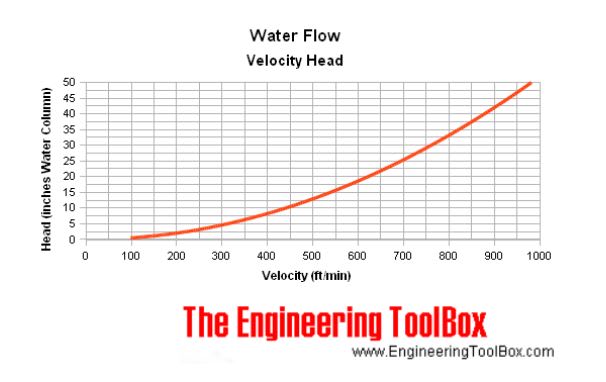
My client's engineer told me "the required test pressure on the roof will be approx. 925kPa". Considering we test 1.5 times of working pressure, the working pressure will be about 600kPa (87psi).
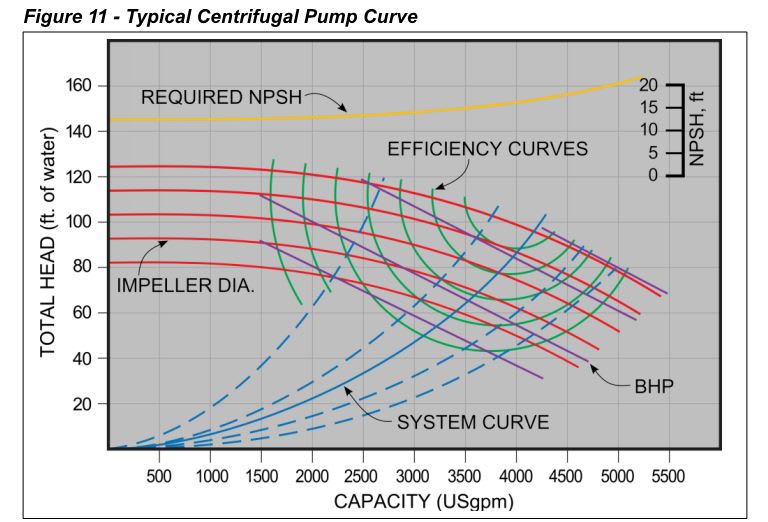
I wonder if 87 psi is a normal pressure for pump head + expansion pre-charge?
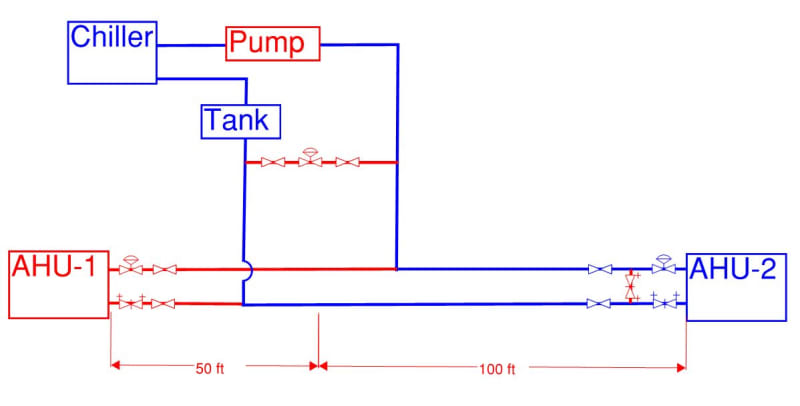
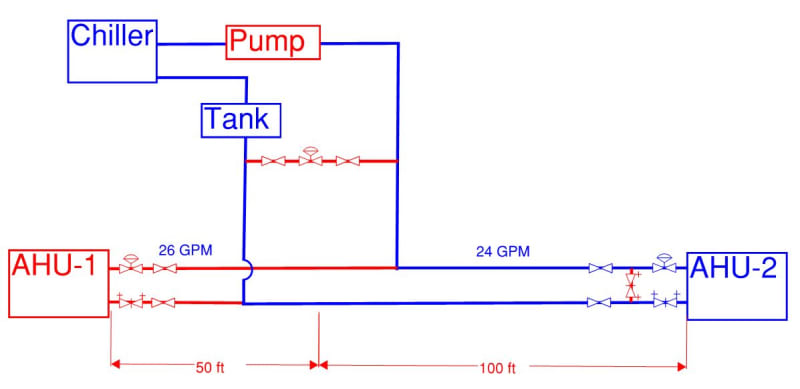
Not sure if this information is useful, but the farthest cooling coil is 130m away from the rooftop plant. (100m elevation & 30m horizontal pipe run)
I'm tendering on a mechanical plumbing job for this building with the air-cooled chillers & all other equipment located on rooftop.
My client's engineer told me "the required test pressure on the roof will be approx. 925kPa". Considering we test 1.5 times of working pressure, the working pressure will be about 600kPa (87psi).
I wonder if 87 psi is a normal pressure for pump head + expansion pre-charge?
Not sure if this information is useful, but the farthest cooling coil is 130m away from the rooftop plant. (100m elevation & 30m horizontal pipe run)