LSUengr2013
Civil/Environmental
- Jul 20, 2020
- 13
My team and I have been contracted to review a PEMB for the installation of some new exhaust fans. These fans are attached to 8" Z-purlins which are through-fastened to an R-panel type metal sheathing.
We have been utilizing RISA-3D to conduct the analysis. When running the analysis, the Z-purlins are failing according to AISI code equation H1.2-1 which is combined axial load and bending.
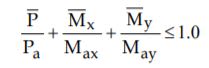
We believe the compression in the purlins is coming from the overall deflection of the main support/girter system and this compressive load is overstressing the member. Reading further into the AISI code, there is a provision for calculation the weak axis compressive strength for a purlin with one flange through fastened to metal sheathing. When we do this calculation by hand, it leads us to a much larger allowable axial compressive force than what RISA is calculating, approximately 7-8x higher. This value also is very close to values found in load tables/charts.
When we insert this hand calculated value into the H1.2-1 equation, the members passes unity. So my question is, could this be a limitation to the programming of RISA and we should rely on our hand calculations for this instance? I do not know of a "factor" within RISA to tell it to default to this equation for allowable axial compression as we are already using Lcomb top, etc.
Any insight into this would be greatly appreciated!
We have been utilizing RISA-3D to conduct the analysis. When running the analysis, the Z-purlins are failing according to AISI code equation H1.2-1 which is combined axial load and bending.
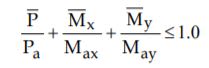
We believe the compression in the purlins is coming from the overall deflection of the main support/girter system and this compressive load is overstressing the member. Reading further into the AISI code, there is a provision for calculation the weak axis compressive strength for a purlin with one flange through fastened to metal sheathing. When we do this calculation by hand, it leads us to a much larger allowable axial compressive force than what RISA is calculating, approximately 7-8x higher. This value also is very close to values found in load tables/charts.
When we insert this hand calculated value into the H1.2-1 equation, the members passes unity. So my question is, could this be a limitation to the programming of RISA and we should rely on our hand calculations for this instance? I do not know of a "factor" within RISA to tell it to default to this equation for allowable axial compression as we are already using Lcomb top, etc.
Any insight into this would be greatly appreciated!

