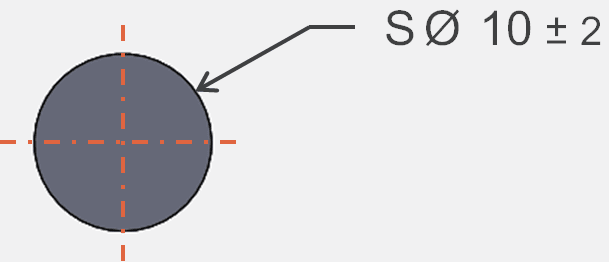
Inner Boundary (IB) of an External Spherical Feature of Size 1

4

Burunduk,

Thank you. I am having a hard time visualizing this one.

Tarator,

The MMC condition establishes an outer boundary of a diameter of 12 (Rule #1). Now imagine if the sphere were produced at LMC size, or a diameter of 8. Imagine that the LMC sphere is on center of the outer boundary. Consider how much that sphere can move within it's outer boundary, knowing the difference between OB size and LMC size. In this case, it can move 2 to the left before hitting the OB, 2 to the right, 2 up, 2 down, etc... The inner boundary will be the area that some part of the sphere will always remain inside, no matter how far it is translated within the boundary. You can see it with a simple 2D analogy, moving the LMC circle left, right, up, and down. I agree with Burunduk that in this case it will be 4.

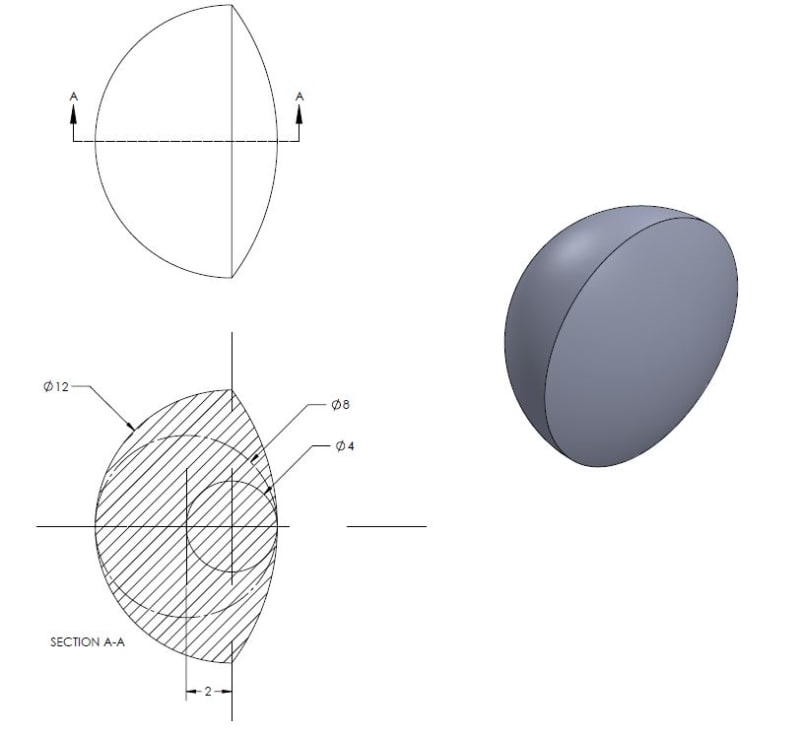
The IB is generated by a combination of the LMC size and the maximum possible form error.

Imagine the sphere is produced at LMC size of 8mm, and there is an indentation at some place on the sphere, 4 mm deep, as the maximum form error allows. To maintain the actual local size requirement, there should be at least 4mm high bump on the opposite side of the sphere. However, if you inscribe a maximum diameter perfect form theoretical sphere within the actual sphere, it will be of 8-4=4mm diameter, because that's the largest sphere that is limited by the indentation. That's your IB.

Isn't it in agreement with the last 3-4 posts in this thread:

Burunduk,
Do you agree with my assessment about IB / OB in the attached discussion? Just curious.

Will somebody enlighten me where ADDITIONAL tolerance comes from?

Per definition,
boundary, inner: a worst-case boundary generated by the smallest feature (MMC for an internal feature and LMC for an external feature) minus the stated geometric tolerance and any additional geometric tolerance (if applicable) resulting from the feature’s departure from its specified material condition.
In OP example NO geometric tolerance is stated and NO material condition is specified.

If OP sphere was located by zero position at MMC, for example, inner boundary could be 4 indeed.
Other then that, I don't see the way for it to be less than 8.

"For every expert there is an equal and opposite expert"
Arthur C. Clarke Profiles of the future

A few things. First I'm not 100% sure the term and concept for IB and OB apply to a feature which only has a size tolerance applied. The definition for IB and OB both seem to require an explicitly applied geometric tolerance applied - as least per the 2009 definition.

Y14.5-2009 said:

1.3.2 Boundary, Inner
boundary, inner: a worst-case boundary generated by the smallest feature (MMC for an internal feature and LMC for an external feature) minus the stated geometric tolerance and any additional geometric tolerance (if applicable) resulting from the feature’s departure from its specified material condition. See Figs. 2-12 through 2-17.

Click to expand...

If we gloss over that, and assume that the concept of IB is applicable in this case (like I said, I'm not convinced it is), then the only way we get a boundary of 4 is if we assume that (1) the boundaries must be coaxial/coincident (ie: share the same center) and/or (2) it is because thats what the calculation provided in the definition says namely LMC minus the available tolerance by deviation from MMC due to rule #1 (MMC-LMC). This is due to the swept spheres interpretation of size - no matter how one evaluates it, including the "bump" mentioned above, you cannot have a situation where you can't fit a sphere of perfect form and LMC size 8 within the as-produced feature otherwise it violates the limits of size (any references to Actual Local Size notwithstanding). See my below figure.

This (the fact that you must be able to fit a sphere of perfect form of minimum LMC size within the as-produced feature) is due to the fact that the nominal shape (sphere) is the same as the shape used to evaluate size (sphere). The behavior is different for cylinders and width shaped features as they are dissimilar to the spherical shape which is used to evaluate size (do not have to fit a cylinder or width of perfect form of LMC size within the as-produced feature).

This said, the definition has changed in 2018 in such a way that I believe is more applicable to features without an explicit geometric tolerance (now says "applicable" geometric tolerance instead of "stated") as well as would support the fact that the IB in the OP case would be 8, as it does not supply a calculation but instead simply states "the collective effects of".

Y14.5-2018 said:

3.2 BOUNDARY, INNER (IB)
boundary, inner: a worst-case boundary generated by the collective effects of the smallest feature of size (MMC for an internal feature of size, LMC for an external feature of size) and the applicable geometric tolerance. See Figures 5-14 through 5-19.

Click to expand...

CH,

Let me ask you this question: do you see how the outer boundary / least material boundary in fig 2.6/2009 could be 20.3?

CH,
You bring up a good point with that quote from the standard, however, I think that if one looks for the absolute worst-case smallest boundary of the external sphere in the OP example it is still 4mm diameter because of the maximum amount of form error allowed by departure from MMC and rule #1. Looks like that's something that wasn't envisioned by the IB term definition.

An envelope of 8mm can only be kept unviolated if perfect form is required at LMC. Nothing in the example specifies that.

Burunduk said:

An envelope of 8mm can only be kept unviolated if perfect form is required at LMC. Nothing in the example specifies that.

Click to expand...

See my above. Its required by the swept spheres definition of size.

chez311,
Exactly my point, I don't see additional tolerances applicable to a feature which only has a size tolerance applied.
Burunduk,
Perfect form being not required at LMC doesn't mean local measurement can be less than 8 at any cross-section.
Greenimi,
I don't see 20.3 anywhere in fig.2.6/2009.
Anyone,
Could you provide a picture of a figure, where cross-section measurement still 8 but inner envelope is limited to 4?

"For every expert there is an equal and opposite expert"
Arthur C. Clarke Profiles of the future

chez311,
I think that if there's an 8mm diameter sphere produced, with a 4mm deep dent opposing a 4mm high bump, that would conform both to the swept spheres definition and to the ALS application of size limits. However, the largest perfect form sphere that can be inscribed in the actual feature is of 4mm diameter. So the current specification can not protect an 8mm boundary.

Ok, I can visualize inner boundary smaller than 8 mm:



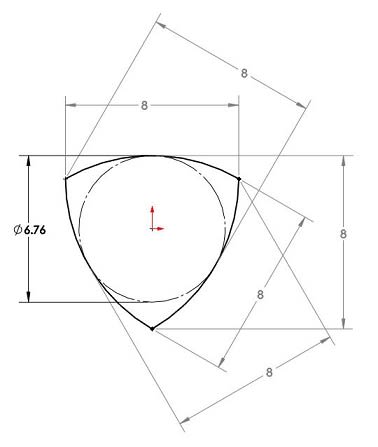
Still far away from 4. Suggestions?

"For every expert there is an equal and opposite expert"
Arthur C. Clarke Profiles of the future

CH said:

Burunduk,
Perfect form being not required at LMC doesn't mean local measurement can be less than 8 at any cross-section.

Click to expand...

I didn't say it can.

CH said:

Still far away from 4. Suggestions?

Click to expand...

Described (for the second time in this thread) in my post from 14:02.

Burunduk said:

I think that if there's an 8mm diameter sphere produced, with a 4mm deep dent opposing a 4mm high bump, that would conform both to the swept spheres definition and to the ALS application of size limits.

Click to expand...

It would not. It would violate your 8mm LMC sphere. The 8mm LMC sphere must be completely inside the material.

If you believe otherwise please provide a sketch that shows it. I do not believe it is geometrically possible, but I am not infallible. I would be interested to be proven wrong.

CH said:

Exactly my point, I don't see additional tolerances applicable to a feature which only has a size tolerance applied.

Click to expand...

Nothing explicit, only implicit by the additional tolerance provided by rule #1 and deviation from MMC size. I agree though, per 2009 definition (requires stated/explicit tolerance) I'm not convinced the concept of IB is even applicable but I went forward sort of glossing over that and applying the concept anyway. The 2018 definition seems to be a different story.

That said, your (6 Aug 20 14:07) violates the limits of size. The 6.76mm circle you show is not possible - that would violate your LMC sphere of 8mm. That circle cannot be any smaller than 8mm, even for feature with trilobular form error.

Burunduk,
You described it twice, but would you be so kind to draw it?
How exactly "dent" and "bump" look like?

"For every expert there is an equal and opposite expert"
Arthur C. Clarke Profiles of the future

chez311,
6.76mm is not a "size" or "measurement"
By definition, perfect form at LMC is not required, so there is no "LMC sphere" it's enough to have "LMC measurements" which are all 8mm.

"For every expert there is an equal and opposite expert"
Arthur C. Clarke Profiles of the future