CivilSigma
Structural
- Nov 16, 2016
- 100
Suppose that a ribbed slab runs over a wall (the rib is perpendicular to the wall), and you want to transfer shear force from the web of the slab to the wall below.
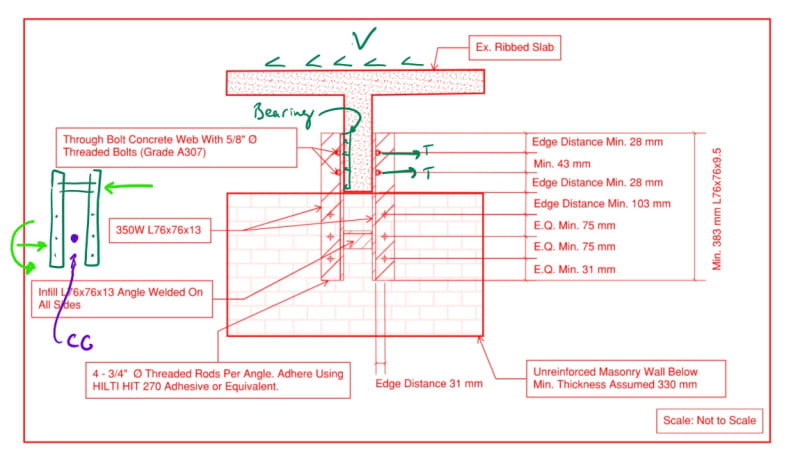
One way to do that is to connect the rib to the wall using a steel angle, bolted to the concrete web on one angle flange, and then bolted to the wall on the other flange as shown in the attached.
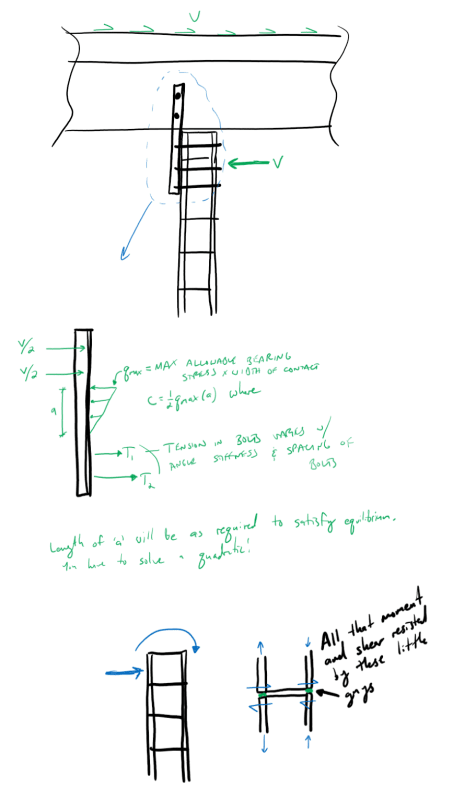
From a geometry perspective, and how the shear force is transferred from the concrete web to the wall below, wouldn't you agree that the bolt assembly in the wall is subject to an eccentric moment: M= Ve, where V is the shear force transferred, and e is the edge spacing of the bolt (31 mm) in this case?
This moment will cause tension (withdrawal) of the bolts in half of the assembly, and must be considered in the bolt design (adhesive capacity in this case).
My colleague believes that if we make the steel angles rigid by adding an infill angle, then we can ignore the effects of the eccentric moment and tension force on the bolts.
I disagree with that and believe that the bolt group will experience tension regardless of how rigid the steel assembly is because they are independent in the assembly and don't rely on the stiffness of the angle.
Following the load path: concrete --> bolts in web --> steel angle ---> bolts in masonry wall (here they will experience tension due to geometrical eccentricity) ---> steel angle (receives eccentricity from the bolts).
Any thoughts?
One way to do that is to connect the rib to the wall using a steel angle, bolted to the concrete web on one angle flange, and then bolted to the wall on the other flange as shown in the attached.
From a geometry perspective, and how the shear force is transferred from the concrete web to the wall below, wouldn't you agree that the bolt assembly in the wall is subject to an eccentric moment: M= Ve, where V is the shear force transferred, and e is the edge spacing of the bolt (31 mm) in this case?
This moment will cause tension (withdrawal) of the bolts in half of the assembly, and must be considered in the bolt design (adhesive capacity in this case).
My colleague believes that if we make the steel angles rigid by adding an infill angle, then we can ignore the effects of the eccentric moment and tension force on the bolts.
I disagree with that and believe that the bolt group will experience tension regardless of how rigid the steel assembly is because they are independent in the assembly and don't rely on the stiffness of the angle.
Following the load path: concrete --> bolts in web --> steel angle ---> bolts in masonry wall (here they will experience tension due to geometrical eccentricity) ---> steel angle (receives eccentricity from the bolts).
Any thoughts?