I have a beam with the following cross-section (due to drawing in paint, the internal circle looks slightly crooked)
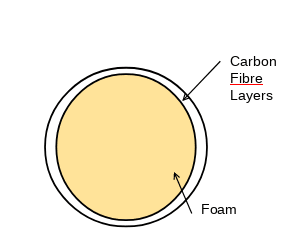
As shown, the outer circle is made of Carbon Fibre layers while the inner region is filled up with foam and cured together. I know the mechanical properties of individual materials. I am interested in estimating Axial stiffness, bending stiffness & torsional stiffness of the beam (cross-section). Is there anyway to determine them using hand calc? Is Classical Laminate Theory valid in the above situation? (Shell of Carbon Fibre layers enclosing a different material). I can try to estimate the above from FEA but just wondering if it can be done via other methods!

As shown, the outer circle is made of Carbon Fibre layers while the inner region is filled up with foam and cured together. I know the mechanical properties of individual materials. I am interested in estimating Axial stiffness, bending stiffness & torsional stiffness of the beam (cross-section). Is there anyway to determine them using hand calc? Is Classical Laminate Theory valid in the above situation? (Shell of Carbon Fibre layers enclosing a different material). I can try to estimate the above from FEA but just wondering if it can be done via other methods!
