Wouterminator
Student
- Nov 23, 2023
- 3
Hello guys,
Im really struggling to do a proper hand calculation for some reason on this really simple frame. none of my methodes seem to solve this one. i need to know what the reaction forces are in the 2 supports at the bottom. Does anyone know something on how to solve this situation? the reaction forces/moments are as you can see already calculated by a simulation.
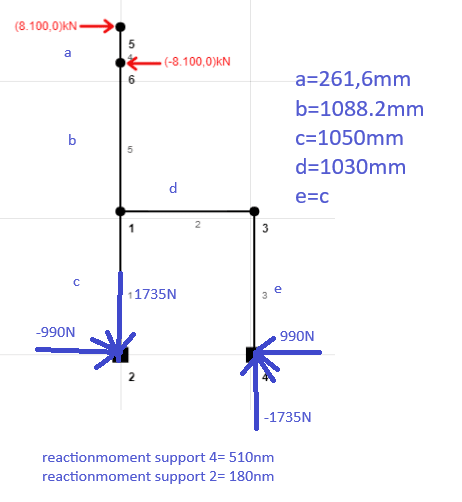
I hope someone can me help out!
Greetings from the netherlands!
Im really struggling to do a proper hand calculation for some reason on this really simple frame. none of my methodes seem to solve this one. i need to know what the reaction forces are in the 2 supports at the bottom. Does anyone know something on how to solve this situation? the reaction forces/moments are as you can see already calculated by a simulation.

I hope someone can me help out!
Greetings from the netherlands!

![[upsidedown] [upsidedown] [upsidedown]](/data/assets/smilies/upsidedown.gif) .
.