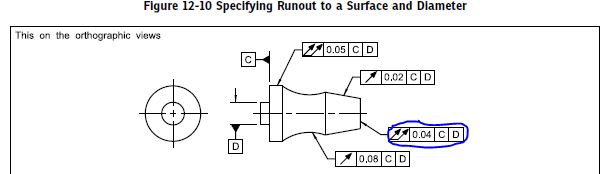
Total run-out interpretation.
I’ve been lurking on this forum for several months and I am impressed with the wealth of knowledge the members bring to the forum. My understanding of the standard has grown as a result. The standard I am referencing in the example is the ASME-Y14.5-2009. For background let me state that the part design is controlled by our customer, with one exception, that is the size of the spherical radius which is under our design control. As such the customer could not use profile to control the spherical radius and instead chose to use total run-out.
My understanding is that run-out, both circular and total, only control radial elements of the feature and not axial. However 9.4.2.1 states that total run-out may be used to control profile of a surface, which has me questioning whether my understanding is correct.
Looking at the example I have several questions:
1. What would a datum simulator for B,A look like? Is this a valid call out or should it be either A,B or just B ( there are no other FCF’s that use B,A so the intent would not be to create a simultaneous requirement)
2. Is this a legitimate use total run-out
3. If #2 is yes, Does total run-out control the 1.00 basic from datum A
I would like to thank everybody in advance for your comments and help.
I’ve been lurking on this forum for several months and I am impressed with the wealth of knowledge the members bring to the forum. My understanding of the standard has grown as a result. The standard I am referencing in the example is the ASME-Y14.5-2009. For background let me state that the part design is controlled by our customer, with one exception, that is the size of the spherical radius which is under our design control. As such the customer could not use profile to control the spherical radius and instead chose to use total run-out.
My understanding is that run-out, both circular and total, only control radial elements of the feature and not axial. However 9.4.2.1 states that total run-out may be used to control profile of a surface, which has me questioning whether my understanding is correct.
Looking at the example I have several questions:
1. What would a datum simulator for B,A look like? Is this a valid call out or should it be either A,B or just B ( there are no other FCF’s that use B,A so the intent would not be to create a simultaneous requirement)
2. Is this a legitimate use total run-out
3. If #2 is yes, Does total run-out control the 1.00 basic from datum A
I would like to thank everybody in advance for your comments and help.