darkjmf1
Structural
- Dec 17, 2012
- 50
Hello,
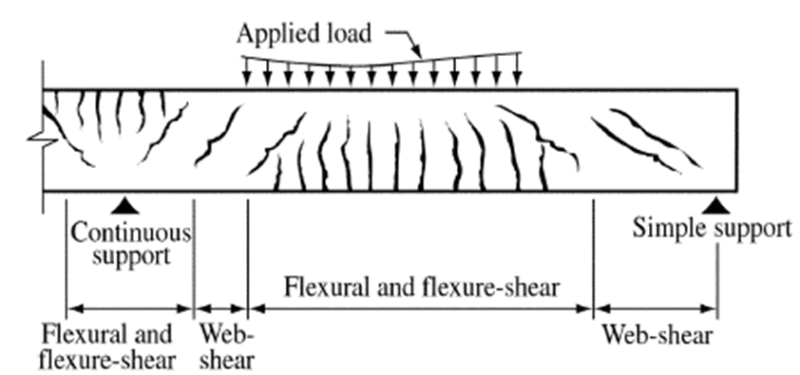
I am designing a RC beam with a section which, due to architectonical reasons, is much larger than required, resulting in minimum reinforcement both for bending and torsion.
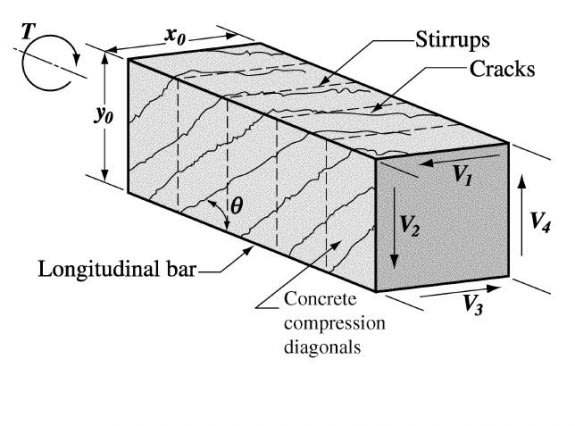
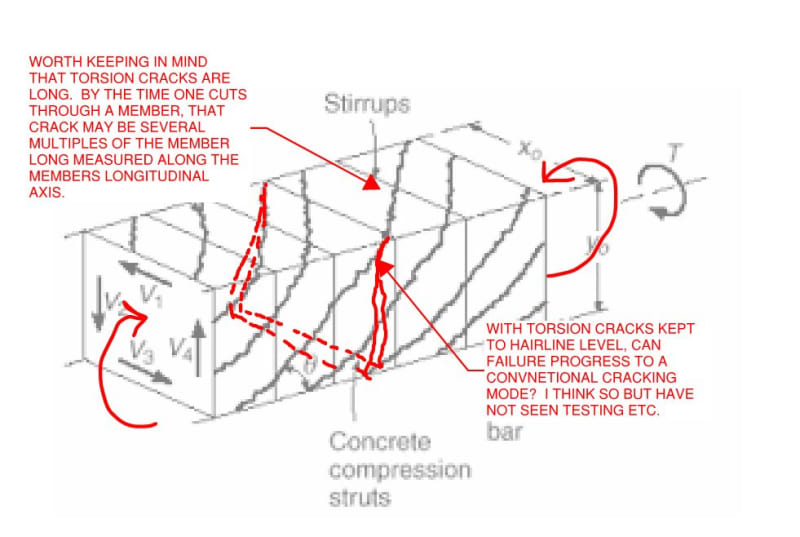
Do I have to calculate both As,min for bending and longitudinal Asl,min for torsion separately and eventually adding them up in the section?
Or could I just calculate both As and Asl required by analysis and just check if the sum of them complies with As,min and Asl,min?
I am using ACI, but I guess this discussion could be applicable for any concrete code.
Thank you all in advance.
I am designing a RC beam with a section which, due to architectonical reasons, is much larger than required, resulting in minimum reinforcement both for bending and torsion.
Do I have to calculate both As,min for bending and longitudinal Asl,min for torsion separately and eventually adding them up in the section?
Or could I just calculate both As and Asl required by analysis and just check if the sum of them complies with As,min and Asl,min?
I am using ACI, but I guess this discussion could be applicable for any concrete code.
Thank you all in advance.