So its been a while since I did beam bending back in school and now I'm having some trouble.
The regular equations, I believe, assume fixed ends, at least the ones I can find. Trouble is I am looking for the length by which a beam gets shorter as it bends, and my end points rotate.
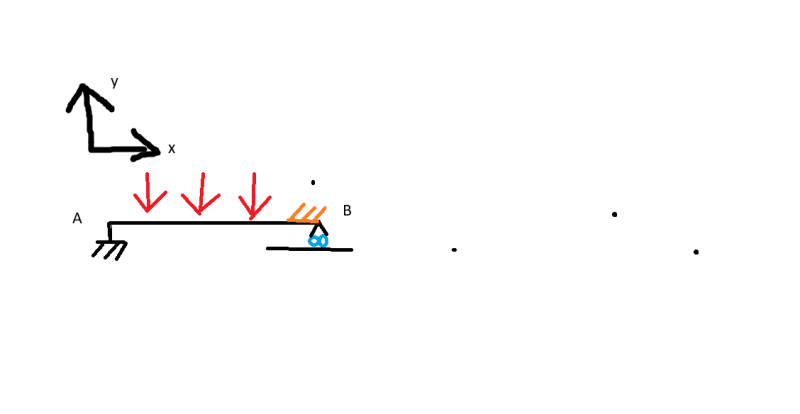
See pic
A is rigidly affixed translationally but allows the beam to rotate freely. B prevents Translation in the Y direction but no other Direction.
I'm trying to make my design driven because we keep changing materials so I'm going with F= force (assuming a uniform load across the length) L= length I=moment of inertia and E= modulus of elasticity.
I tried finding the deformation with (5*F*L^4)/(384*E*I)=d. and then the slope with w*L^3/(24*E*I). and using those to back out the geometry of the arc but the math isn't right.
Am I heading in the right direction?
Any help would be a life saver
The regular equations, I believe, assume fixed ends, at least the ones I can find. Trouble is I am looking for the length by which a beam gets shorter as it bends, and my end points rotate.
See pic
A is rigidly affixed translationally but allows the beam to rotate freely. B prevents Translation in the Y direction but no other Direction.
I'm trying to make my design driven because we keep changing materials so I'm going with F= force (assuming a uniform load across the length) L= length I=moment of inertia and E= modulus of elasticity.
I tried finding the deformation with (5*F*L^4)/(384*E*I)=d. and then the slope with w*L^3/(24*E*I). and using those to back out the geometry of the arc but the math isn't right.
Am I heading in the right direction?
Any help would be a life saver