TEDstruc
Civil/Environmental
- Dec 6, 2017
- 43
IN THE ATTACHED DIAGRAM, ASSUMING THE PLATES ARE CONTINUOUS IN AND OUT OF THE PAGE, WILL THE PLATES BEHAVE LIKE A COMBINED SECTION?
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
TEDstruc said:but with the weld at the free end, I wasn't sure since the plates aren't really free to slip independently.
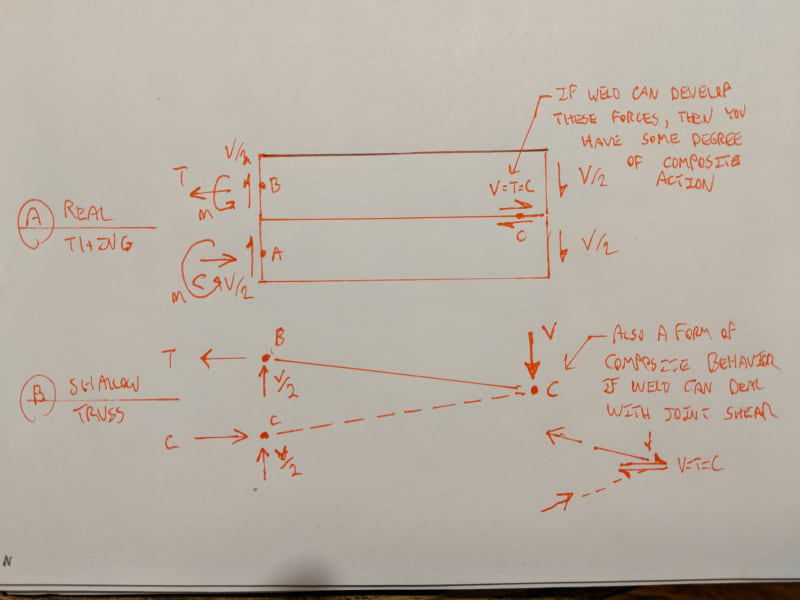
..the question in my mind is what force would one design the weld @ the tip for?....at first glance, I thought that if one designed it for the shear assuming full composite action that it would be conservative and ok....but, on further thought. there is also the force from the individual bending of each pl being constrained to act as one @ the tip....I have no clue at the moment on what the magnitude of that would be.....
SAIL4 said:the question in my mind is what force would one design the weld @ the tip for?
The load sharing component will be negligible relative to the faux composite demand.
WARose said:.and the piece that connected the 2 cantilevers had a axial load of V/2 (by your sketch).
V/2 is what I would expect for that component. I'd probably just design it for V. My point is that I would expect the shear flow component to be much larger than that and, looking back at my shallow truss model, that seems pretty apparent to me.
WARose said:According to my model, it depends on how long that connector is.
Structural Wiz said:In order for KootK's sketch to apply, you would have to weld the top plate and bottom plate to the support!
BAret said:How did we get V = T = C on Kootk's Sketch B?
