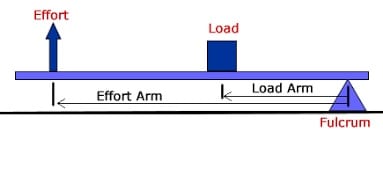
I am analyzing a system that can be modeled as a 2nd class fulcrum. The link below about 1/3 of the way down the page shows an example of a 2nd class fulcrum.
2nd class fulcrum Link
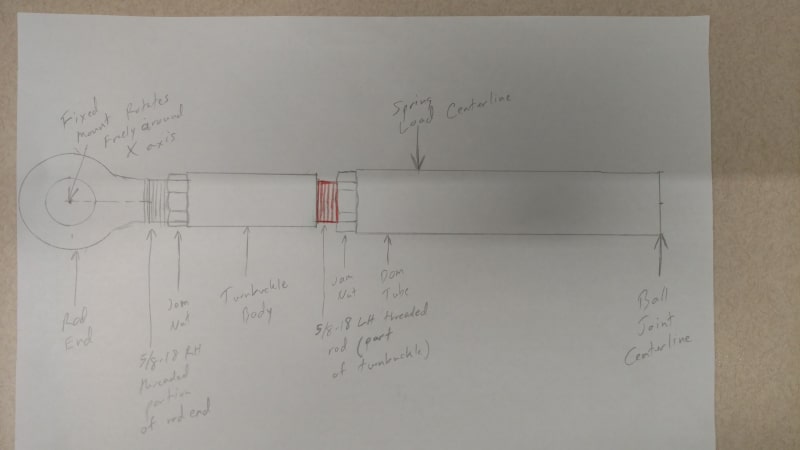
The part that makes up the beam is a composite part made up of a turnbuckle (see link below), threaded tube and a rod end/heim joint that have different cross sections. The beam has a turnbuckle where part of it is a solid male LH threaded rod and part of is a female RH threaded tube. The male portion of the turnbuckle threads into a different threaded tube and the female portion of the turnbuckle has a male threaded rod end/heim joint screwed into it.
Turnbuckle Link
I know the fulcrum arm length, load arm length load, load amount and the moment of inertia of each of the individual portions, but i'm not quite sure if I can calculate an overall moment of inertia of the beam to analyze the stress and deflection of the entire beam as a whole or if I need to determine the load/bending moment at each unique portion of the beam and analyze each section of the beam separately. Any help would be appreciated. Thanks
TC
Comm and GPS Systems Engineer
2nd class fulcrum Link
The part that makes up the beam is a composite part made up of a turnbuckle (see link below), threaded tube and a rod end/heim joint that have different cross sections. The beam has a turnbuckle where part of it is a solid male LH threaded rod and part of is a female RH threaded tube. The male portion of the turnbuckle threads into a different threaded tube and the female portion of the turnbuckle has a male threaded rod end/heim joint screwed into it.
Turnbuckle Link
I know the fulcrum arm length, load arm length load, load amount and the moment of inertia of each of the individual portions, but i'm not quite sure if I can calculate an overall moment of inertia of the beam to analyze the stress and deflection of the entire beam as a whole or if I need to determine the load/bending moment at each unique portion of the beam and analyze each section of the beam separately. Any help would be appreciated. Thanks
TC
Comm and GPS Systems Engineer