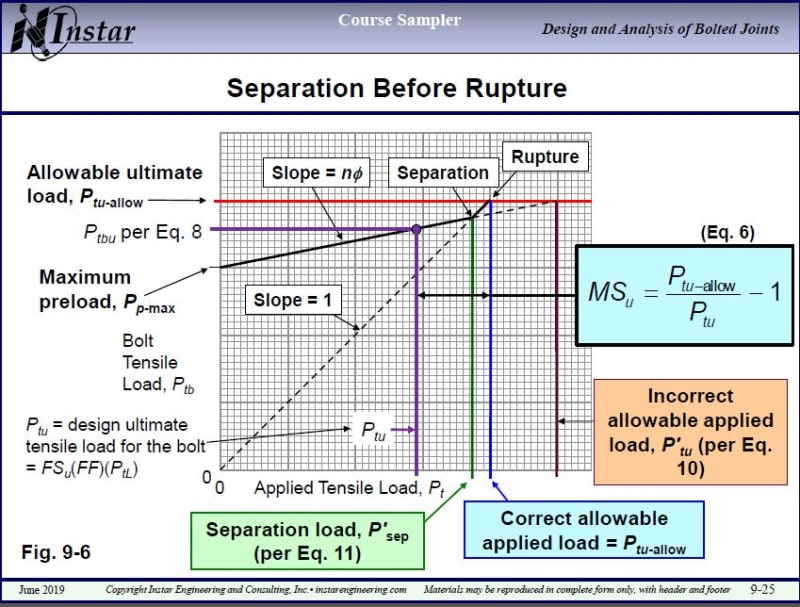
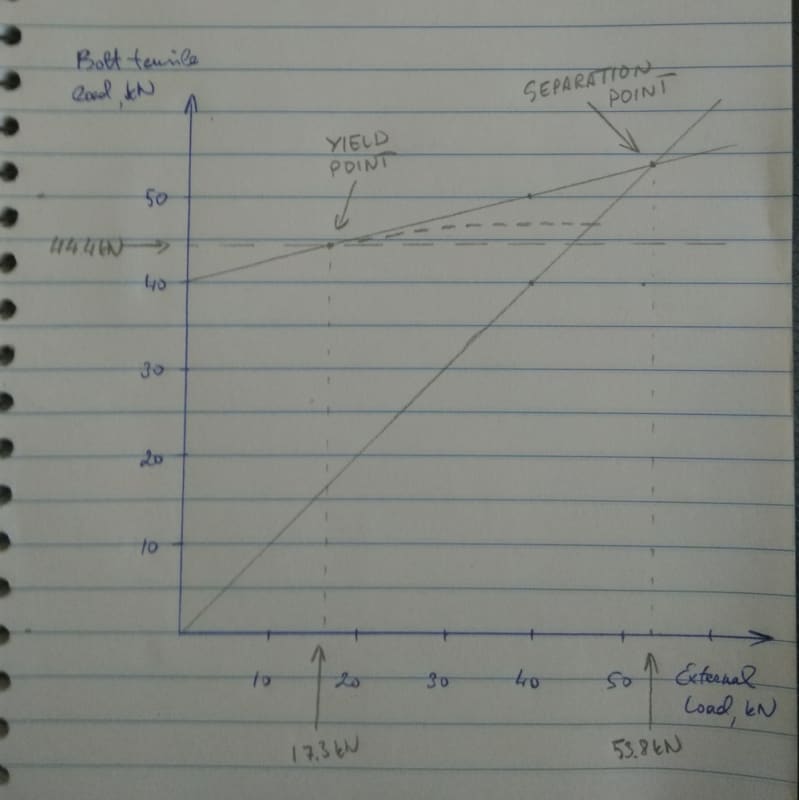
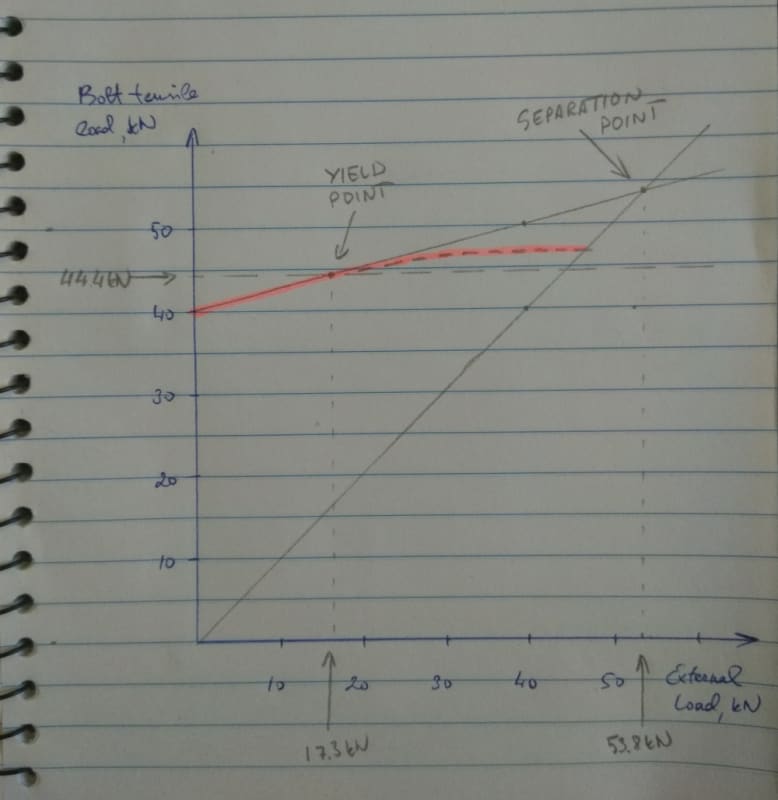
-
1
- #1
Hi all,
I hope its not a stupid question, or if it is then maybe someone can point towards that "simple and obvious" answer that I'm failing to see here! Here goes:
I haven't got much experience with bolted joints, so far simple guidelines such as VDI2230 have helped me out just fine.
However, now I was trying to use VDI2230 for determining the tightening torques for a bolted flange and came across something that I fail to make sense of.
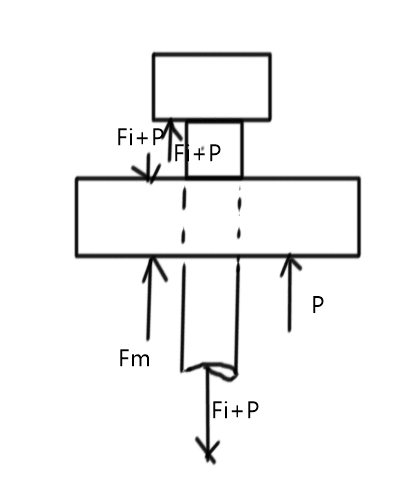
I'll give you a simplified description. It's a pipe with a flange, and an end cap bolted onto it to seal it off. Lets say it has 4 bolts that are evenly spread along the diameter, or 90degrees apart from each other. The holes in the flanges are not threaded, just bolts through and and nuts on the other side.
I'll use the VDI2230 method for calculating these bolts, following the procedure I found in a Würth publication.
Based on the diameter of the pipe and maximum working pressure I have determined that the maximum force on the cap will be 9.2 kN, that makes 2.3 kN per each of the 4 bolts. Therefore the axial operating force Fa = 2.3 kN.
As I have no shear forces to consider, the assembly preload force Fm = Fa = 2.3 kN. This will be my starting point.
Let's say I want to use grade 8.8 bolts. Looking at the VDI2230 table, the next closest load there is 2.5 kN -> size M4 is specified for 8.8 bolts.
Add one step for static concentric load -> 4.0 kN -> M5
Add one step for tightening with a torque wrench -> 6.3 kN -> M6
So the bolts that I need are grade 8.8 size M6.
I will estimate the coefficient of friction to be 0.11. The next closest step in the guidelines I have is 0.10, so lets got with that.
Based on all this, VDI2230 advises me that the tightening torque would be Ma = 9.0 Nm, which would create a 10.4 kN preload force in the bolt. It is said to utilize 90% of the screws yield strength.
Based on my calculation, the breaking load of a M6 8.8 coarse thread bolt at yield strength (640 MPa) is 11.29 kN.
10.4 / 11.29 = 92%, so that's just about right.
But... the assembly is not pressurized when I'm tightening those bolts. By just tightening them, I've already used up 92% of the bolts' reserve, not much left for when I will actually pressurize it.
If i will now calculate how much pressure this assembly can take after tightening the bolts, then I can only use the reserve left in the bolts (8 percent to yield strength) as in my calculation? That's not much...
Or lets give you another really simple example just to illustrate the point I'm trying to make here:
Lets say you have an M6 eye bolt, you insert it through a hole in a rigid steel plate in the ceiling, and screw a nut on the other side. If the nut is not tightened, then you can hang 11.29 kN load on your eye bolt before it breaks, but after you've tightened the nut according to VDI2230, you can only hang 11.29 kN x 8% = 0.9 kN off it before it snaps!.
I'm kinda confused here. What am I missing? All the example calculations I have seen for pressurized flanges, lids, end caps on pressure vessels etc just use the full capacity of the bolts in their strength calculations. But how can I do that if I've already used up 9/10 of it???
Could I tighten the nuts to a lesser torque than specified? But wouldn't the flange then leak, and would the bolts rattle loose / become undone too easily?
Thanks for any feedback (or for proving me stupid, it that happens to be the case
J.
I hope its not a stupid question, or if it is then maybe someone can point towards that "simple and obvious" answer that I'm failing to see here! Here goes:
I haven't got much experience with bolted joints, so far simple guidelines such as VDI2230 have helped me out just fine.
However, now I was trying to use VDI2230 for determining the tightening torques for a bolted flange and came across something that I fail to make sense of.
I'll give you a simplified description. It's a pipe with a flange, and an end cap bolted onto it to seal it off. Lets say it has 4 bolts that are evenly spread along the diameter, or 90degrees apart from each other. The holes in the flanges are not threaded, just bolts through and and nuts on the other side.
I'll use the VDI2230 method for calculating these bolts, following the procedure I found in a Würth publication.
Based on the diameter of the pipe and maximum working pressure I have determined that the maximum force on the cap will be 9.2 kN, that makes 2.3 kN per each of the 4 bolts. Therefore the axial operating force Fa = 2.3 kN.
As I have no shear forces to consider, the assembly preload force Fm = Fa = 2.3 kN. This will be my starting point.
Let's say I want to use grade 8.8 bolts. Looking at the VDI2230 table, the next closest load there is 2.5 kN -> size M4 is specified for 8.8 bolts.
Add one step for static concentric load -> 4.0 kN -> M5
Add one step for tightening with a torque wrench -> 6.3 kN -> M6
So the bolts that I need are grade 8.8 size M6.
I will estimate the coefficient of friction to be 0.11. The next closest step in the guidelines I have is 0.10, so lets got with that.
Based on all this, VDI2230 advises me that the tightening torque would be Ma = 9.0 Nm, which would create a 10.4 kN preload force in the bolt. It is said to utilize 90% of the screws yield strength.
Based on my calculation, the breaking load of a M6 8.8 coarse thread bolt at yield strength (640 MPa) is 11.29 kN.
10.4 / 11.29 = 92%, so that's just about right.
But... the assembly is not pressurized when I'm tightening those bolts. By just tightening them, I've already used up 92% of the bolts' reserve, not much left for when I will actually pressurize it.
If i will now calculate how much pressure this assembly can take after tightening the bolts, then I can only use the reserve left in the bolts (8 percent to yield strength) as in my calculation? That's not much...
Or lets give you another really simple example just to illustrate the point I'm trying to make here:
Lets say you have an M6 eye bolt, you insert it through a hole in a rigid steel plate in the ceiling, and screw a nut on the other side. If the nut is not tightened, then you can hang 11.29 kN load on your eye bolt before it breaks, but after you've tightened the nut according to VDI2230, you can only hang 11.29 kN x 8% = 0.9 kN off it before it snaps!.
I'm kinda confused here. What am I missing? All the example calculations I have seen for pressurized flanges, lids, end caps on pressure vessels etc just use the full capacity of the bolts in their strength calculations. But how can I do that if I've already used up 9/10 of it???
Could I tighten the nuts to a lesser torque than specified? But wouldn't the flange then leak, and would the bolts rattle loose / become undone too easily?
Thanks for any feedback (or for proving me stupid, it that happens to be the case
J.



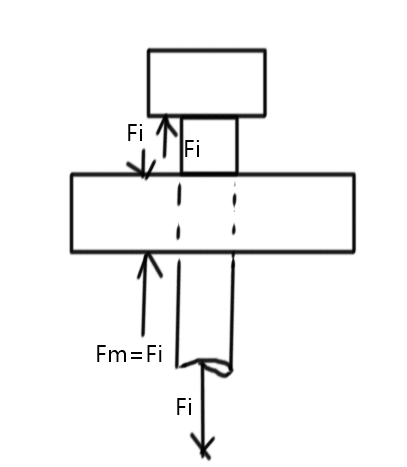
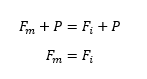

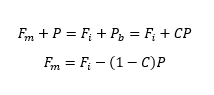
![[upsidedown] [upsidedown] [upsidedown]](/data/assets/smilies/upsidedown.gif)