novembertango88
Civil/Environmental
- Feb 11, 2020
- 35
Hi all,
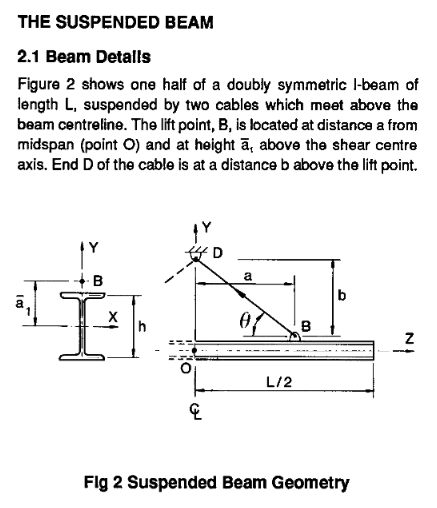
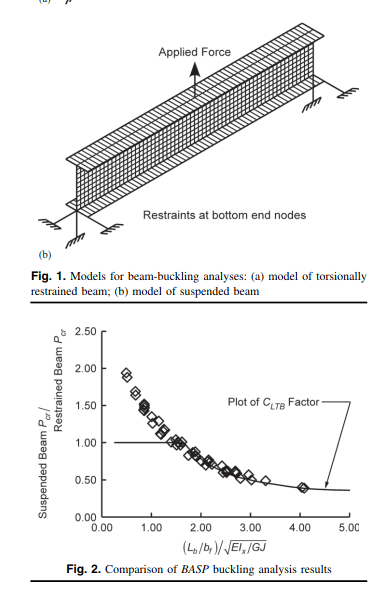
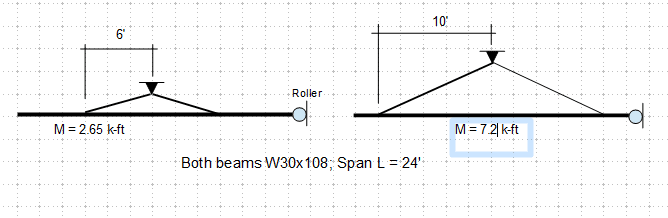
I have a beam hanging from rods as shown in the attached sketch.
What do I take for the buckling length?
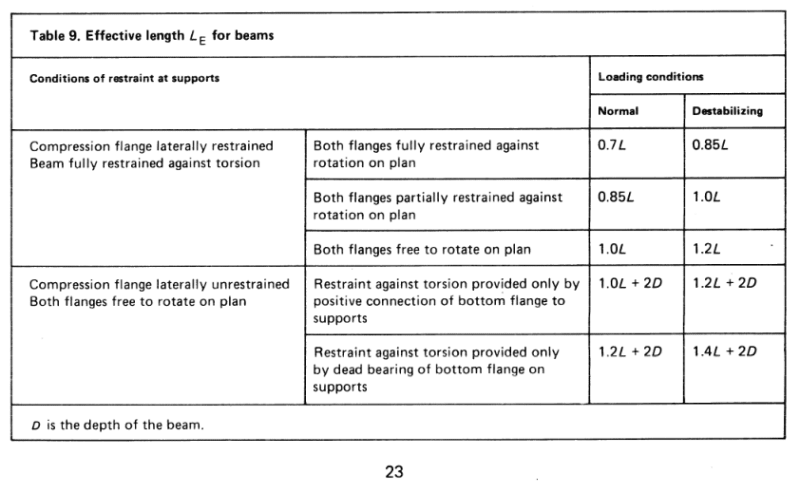
The load is on the top compression flange so I'm considering it destabilizing, the compression flange has no lateral restraint and no torsional restraint. BS 5950-1 table 13 gives a value of 1.4*L(length)+2*D(depth).
Does this sound right?
Thanks, Nick
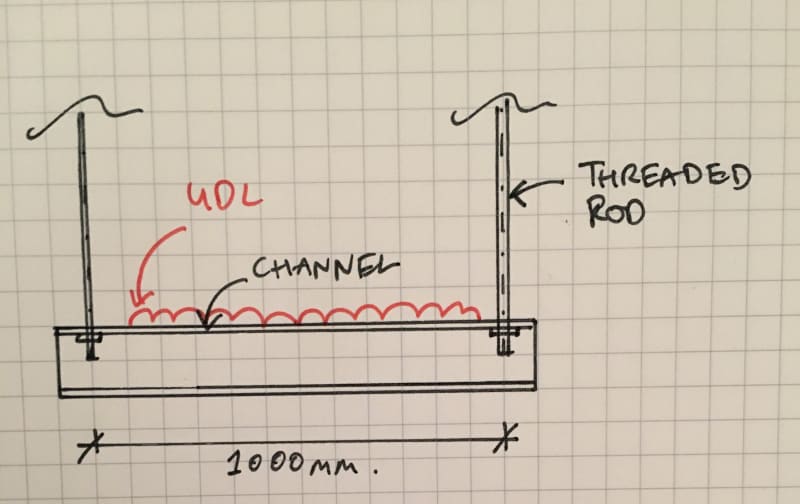
I have a beam hanging from rods as shown in the attached sketch.
What do I take for the buckling length?
The load is on the top compression flange so I'm considering it destabilizing, the compression flange has no lateral restraint and no torsional restraint. BS 5950-1 table 13 gives a value of 1.4*L(length)+2*D(depth).
Does this sound right?
Thanks, Nick