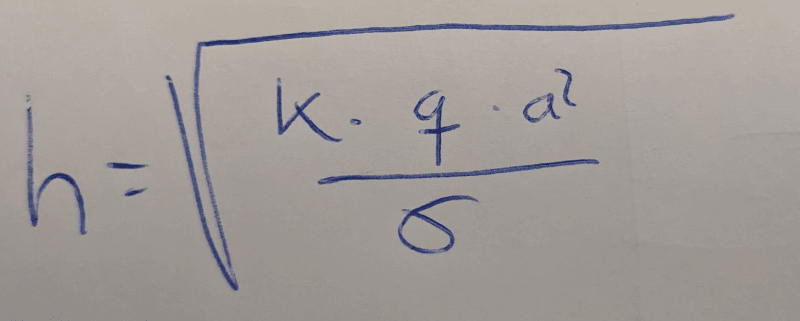drodrig
Mechanical
- Mar 28, 2013
- 262
Hi,
I wrote some time ago asking for and end-cap to close a vacuum volume. I learnt a lot from that post and now I am bringing a similar case.
After some calculations I wanted to present the new case here. Checking the results there are some results that make no sense and it is because this formula:
(From the Timoshenko book, Theory of plates and shells)

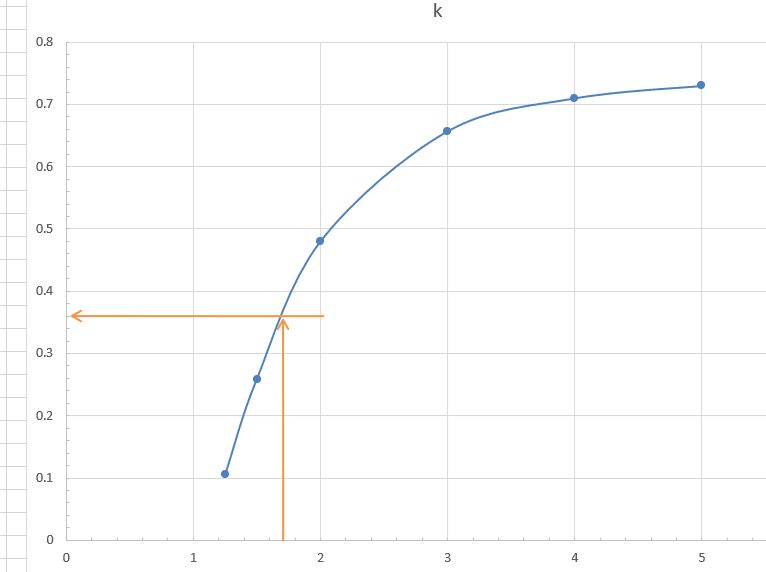
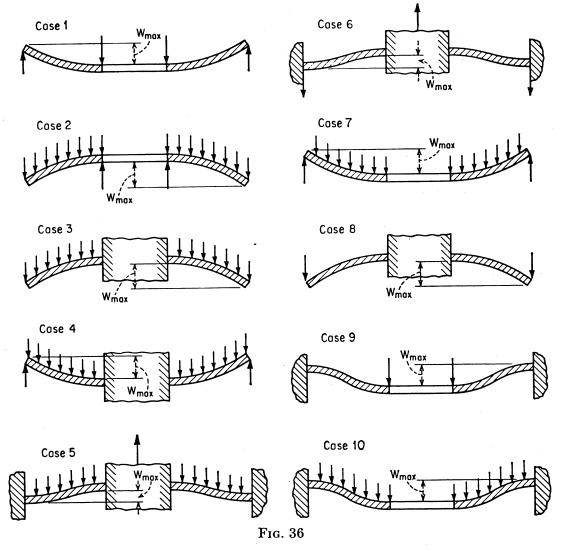
The value of "k" comes from this table and these cases:
("a" is the biggest and "b" the smallest radius of the bulkhead)
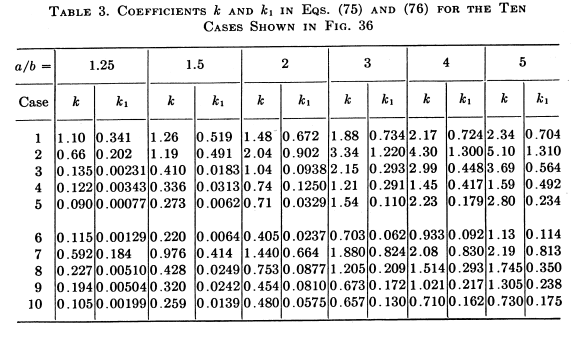
In the formula, the value of "k" grows when the ratio "a/b" grows. Which means that the maximum stress grows too.
Let's suppose two scenarios of the case 10 (plate clamped in the outer perimeter
Scenario A
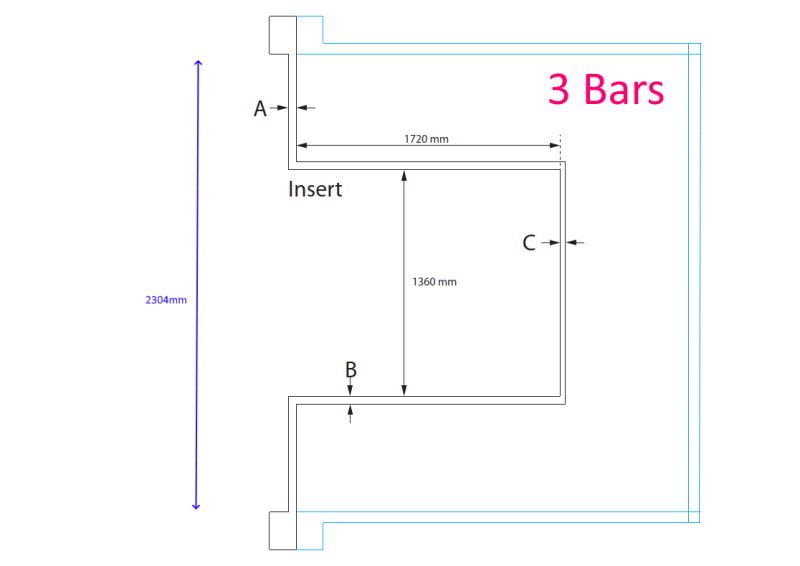
Outer radius: 1150mm
Inner radius: 680 mm
ratio a/b: 1.70
value k: 0.365 (case 10, interpolating)
area: 2.7e6 mm2
Scenario B
Outer radius: 680mm
Inner radius: 25 mm
ratio a/b: 27.2
value k: 0.75 (case 10, extrapolating, it is asymptotic)
area: 1.4e6 mm2 (almost half)
How is it possible that the scenario B has higher stress (higher "h" value) when the area is almost half?
Because of the longer (clamped) perimeter of the scenario A?
thanks
regards,
I wrote some time ago asking for and end-cap to close a vacuum volume. I learnt a lot from that post and now I am bringing a similar case.
After some calculations I wanted to present the new case here. Checking the results there are some results that make no sense and it is because this formula:
(From the Timoshenko book, Theory of plates and shells)

The value of "k" comes from this table and these cases:
("a" is the biggest and "b" the smallest radius of the bulkhead)


In the formula, the value of "k" grows when the ratio "a/b" grows. Which means that the maximum stress grows too.
Let's suppose two scenarios of the case 10 (plate clamped in the outer perimeter
Scenario A
Outer radius: 1150mm
Inner radius: 680 mm
ratio a/b: 1.70
value k: 0.365 (case 10, interpolating)
area: 2.7e6 mm2
Scenario B
Outer radius: 680mm
Inner radius: 25 mm
ratio a/b: 27.2
value k: 0.75 (case 10, extrapolating, it is asymptotic)
area: 1.4e6 mm2 (almost half)
How is it possible that the scenario B has higher stress (higher "h" value) when the area is almost half?
Because of the longer (clamped) perimeter of the scenario A?
thanks
regards,