ochy38
Structural
- Aug 18, 2024
- 10
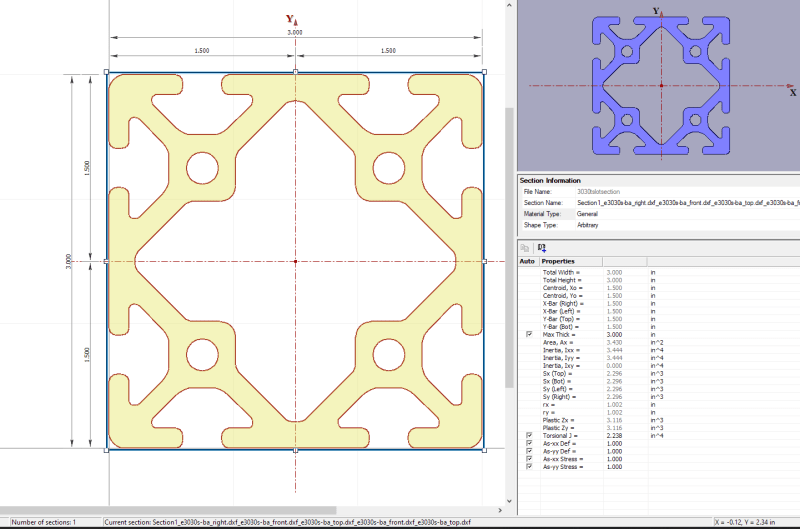
Im working on a beam problem that has my head spinning. It is an 8' beam with a splice 2' in along the span. The outer beam is a square aluminum tube and the inner sleeve is a solid piece of aluminum. I am trying to figure out the capacities of the bolts, the holes in the sleeve, and the holes in the beam.
Figuring out the stress due to bending at a certain spot along the tube or sleeve is easy enough, σ=My/I. That leaves me with a PSI unit. It's easy enough to convert that to a shear value for the bolt with its area.
Originally, the bolts were horizontal. I was able to easily calculate the stress using the above equation, at the farthest edge of the bolt from centroid, and taking the cross sectional area of material of either the tube or sleeve to determine a shear capacity of that part.
Now, with the bolts vertical, I am somewhat confused on how to find the capacities. It doesnt seem as straight forward as "max stress is this" and "stress acts on this cross sectional area", as the stress isnt a specific value. And what area would it actually act upon?
Appreciate any thoughts! I am aways removed from college and haven't done a problem like this in some time.
Figuring out the stress due to bending at a certain spot along the tube or sleeve is easy enough, σ=My/I. That leaves me with a PSI unit. It's easy enough to convert that to a shear value for the bolt with its area.
Originally, the bolts were horizontal. I was able to easily calculate the stress using the above equation, at the farthest edge of the bolt from centroid, and taking the cross sectional area of material of either the tube or sleeve to determine a shear capacity of that part.
Now, with the bolts vertical, I am somewhat confused on how to find the capacities. It doesnt seem as straight forward as "max stress is this" and "stress acts on this cross sectional area", as the stress isnt a specific value. And what area would it actually act upon?
Appreciate any thoughts! I am aways removed from college and haven't done a problem like this in some time.