Melad Saad
Structural
- Jan 3, 2020
- 8
Dear All,, Hope you could help me with this...
I need to work on design optimisation of steel space structures, using Continuous design variables. I am using different sections from that in the Universal Tables (UBs & UCs) by assuming new section dimensions.
I would like to know to calculate the following section properties of Universal Steel Beams and Columns:
- Second moment of area (Iy and Iz)
- Radius of gyration (iy and iz)
- Elastic modulus (Wel.y & Wel.z)
- Plastic modulus (Wpl.y & Wpl.z)
- Warping constant (Iw)
- Torsional constant (It)
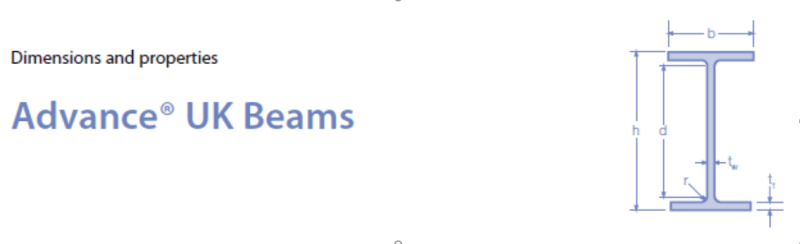
I need to work on design optimisation of steel space structures, using Continuous design variables. I am using different sections from that in the Universal Tables (UBs & UCs) by assuming new section dimensions.
I would like to know to calculate the following section properties of Universal Steel Beams and Columns:
- Second moment of area (Iy and Iz)
- Radius of gyration (iy and iz)
- Elastic modulus (Wel.y & Wel.z)
- Plastic modulus (Wpl.y & Wpl.z)
- Warping constant (Iw)
- Torsional constant (It)