Cantilever retaining wall with narrow site cut 3

[bhiggins]

Hi all!

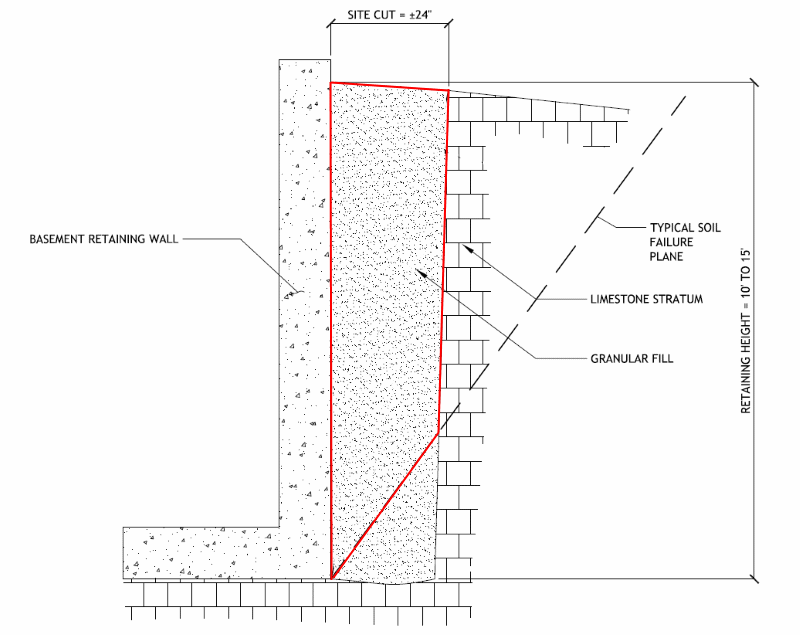
I've got a project here where a basement retaining wall is being loaded with only 2-3 feet width of backfill. The site is on hard limestone so the cut is nearly vertical. The geo report provides active and at rest EFP. Since this is not a standard retaining condition, I'm wondering if these EFP can be reduced based on my situation.

If so, is it appropriate to use a different angle of internal friction or some other rational method? Can this be done without the geo recalculating the EFP for me? I'm just wondering for the future if this can be done without geotechnical intervention.

My guesses are that either the EFP is lower, or the EFP remains the same and the load resembles a triangular distribution that is "capped" off at some point, resulting in a triangular load to a uniform load.

 

[JoelTXCive]

I agree that even with your 10'-15' height, you are barely retaining anything.

We often have imperfect or missing geotech data on walls that we do. In such cases, we will assume a k_active of .5, which is pretty high. We'll also keep the bearing pressure under 1,500psf. We then generate a design and compare to standard designs published by TxDot. (I think Florida and California have published designs too.)

Link

http://www.dot.state.tx.us/insdtdot/orgchart/cmd/cserve/standard/bridge-e.htm#RETAININGWALLS

If you take that approach, you can save the geotech money, but you might end up with an overly conservative design.

 

[SlideRuleEra]

I'm wondering if these EFP can be reduced based on my situation.

Unfortunately, no. The EFP is calculated based on the granular fill's unit weight and angle of repose. These two properties do not change with horizontal thickness. The EFP calcs "transform" the effective properties of a "heavy" granular solid into a "light" liquid. This "light" liquid now is assumed to act like a "real" liquid, say, water.

Consider your project, if the substance being retained was actually water (instead of granular fill), the hydrostatic pressure on the wall would be exactly the same even if the horizontal distance was 2 feet or 2 inches or 2 miles. The same reasoning applies for an "equivalent fluid".

http://www.SlideRuleEra.net

http://www.VacuumTubeEra.net

 

[ATSE]

With hesitation, I respectfully disagree with SRE.
If water, then yes, width behind wall is unimportant unless seismic is considered.
However, the very simplified equivalent fluid pressure analogy for soil is no longer valid for thin backfill strips (column of soil). Total backfill weight and friction are relevant.
Having said that, I would proceed with caution and conservatism. Walls and backfill are never wished into place. Consider the saturated condition and potential pore water pressure, and how the backfill is placed and/or compacted, and the resulting lateral pressures may be similar to conventional construction.
For low volume, you may be better off backfilling with 4 foot lifts of CLSM ("CDF" / 2-sack slurry).

 

[bhiggins]

To me the fluid analog is based on the assumption that a "wedge" of soil will fail and push against the wall. This "wedge" area will increase linearly with wall height thus behaving "like" a fluid which makes the equations work. I'm not sure if this analogy can be used in all situations based on soil mechanics which I do not fully understand.

It seems to me that this "wedge" has been altered thus we need to alter our design method.

 

[SAIL3]

sliderule....would the hydrostatic pressure be the same if the distance/gap was , say 1/8"...a condition that could easily exist due to soil/backfill schrinkage combined with a sudden rain storm....a colleague posed the question awhile back and there was no conclusive opinion on it.....

 

[bhiggins]

For low volume, you may be better off backfilling with 4 foot lifts of CLSM ("CDF" / 2-sack slurry).

Unfortunately there is a lot of basement wall and fill, so this would not be a cost effective option. This wall is being constructed now. There is a PVC drain pipe and a Miradrain waterproofing system. And I did end up designing with the full EFP in the end just to be safe.

I just wanted to bring this up for discussion in case this situation comes up again.

 

[SlideRuleEra]

I though my response would be controversial... that's good.

ATSE - I won't dispute that there are other methods, besides EFP, to compute the force on a retaining wall. But the OP is working with EFP values. Since that is what is available, the simplifications and limitations that go with an EFP approach can not be ignored. If the granular backfill is going to be "transformed" to an equivalent fluid, then the equations that apply to true fluids must be followed.

sail3 - Absolutely. For a horizontal gap that is continuous from top to bottom, a measurement of 1/8" (or less) will put full hydrostatic pressure on the wall. Here is an example:

Assume water weighs 62.4 lb/ft[sup]3[/sup]

Water pressure (lb/ft[sup]2[/sup]) depends on ONLY one variable, the water depth. For a 10' high wall, pressure is 624 lb/ft[sup]2[/sup].

The force per foot of wall length (from water alone) is depends only on the water depth. For the 10' high wall that is P[sub]w[/sub] = 1/2 (62.4 lb/ft[sup]3[/sup]) (10 ft.)[sup]2[/sup] = 3120 lb / foot of wall length.

Note that nowhere does the horizontal distance (1/8", per your question) enter into the equations.

The combined force on the wall from the water's hydrostatic pressure plus the soil behind the wall can get more complicated... the soil may be submerged instead of being "dry".

bhiggins - I've marked up your drawing (see below). If the wall was suddenly removed, the granular fill outlined in red is what would collapse. Note that this occurs along the "typical soil failure plane". Soil properties define that plane, not the horizontal dimension.

http://www.SlideRuleEra.net

http://www.VacuumTubeEra.net

 

[SAIL3]

SRE....if one takes this to a possible(practical) limit...1/32", 1/64", etc....my engineering instinct struggles with accepting this and honestly can not explain why, at the moment....this is not implying that you are incorrect in any way, just my struggle with the concept when it approaches a minute gap.......

 

[SlideRuleEra]

SAIL3 - No offense taken. This is a difficult concept to accept, but it is true. If the horizontal measurement is important... why isn't there a term for the horizontal measurement in the hydrostatic equations?

If 24" (horizontal) is "ok" but 1/64" (horizontal) is not... exactly where does the change happen? The equations would have to define that situation, but they don't. Horizontal distance is not a factor.

In "real life", I do accept that a continuous 1/64" wide gap that is 10' (or so) tall is unlikely. In that case, it's not the theory or the equations that are wrong, it's just that other issues override them.

http://www.SlideRuleEra.net

http://www.VacuumTubeEra.net

 

[JoelTXCive]

I have a related question on L-shaped cantilevered retaining walls, but I don't want to hi-jack this thread, so I'll start a new one.

 

[wannabeSE]

Since I am not a geotechnical engineer, I would contact the geotech who prepared the report rather than a bunch of structural engineers on the internet. He is the one who recommended the design loads for this site with limestone.

 

[pappyirl]

If the cut on the limestone is vertical, then the assumption would be that there is no load from the limestone on the retaining wall. So the retaining wall is retaining the fill that you are adding. I must be missing something but why is the retaining wall required in the first place? Could a liner wall, insulation and a drain to prevent build up of water behind the wall not perform the same role. Or do we assume the drain might not be reliable and design for a hydrostatic load?

SRA - The thrust on the wall is a function of the vertical load behind the wall e.g. consider a surcharge at the top of the wall. A 1/64" gap filled with a column of water cannot produce the same thurst as say as a 6 foot gap fIlled with a column of water, assuming the limestone is impermeable, the thrust would be magnitudes greater that the weight of the column. I would suggest the equations are assuming the depth behind the wall is considered part of a continuous medium which would be typical, so maybe not applicable in this case.

 

[Okiryu]

Perhaps this old thread helps:

http://www.eng-tips.com/viewthread.cfm?qid=197530

 

[Okiryu]

The paper from Frydman indicated in one of the threads is available in internet. Just google the title of the paper.

 

[SlideRuleEra]

pappyirl - On a 10' high wall what horizontal thrust do you get for a water filled gap that is 1/64" wide compared to a 6' wide gap?

For water at 62.4 lb/ft[sup]3[/sup], I get 3120 lb/foot of wall length in both cases.

If there are other equations for special cases of water pressure I would like to know what they are.

http://www.SlideRuleEra.net

http://www.VacuumTubeEra.net

 

[chris3eb]

SRE, I'm not sure about in this specific situation, but in general I don't think its correct to say that just because an equation doesn't have a term in it, that term doesn't matter. Often times simplifications are made to equations make them more workable and this is valid for normal ranges. But as you start going to the fringes, terms that are usually ignored may become important.

 

[jayrod12]

SRE is correct, it seems counter intuitive I know. My hydraulics teacher spent a full two days driving this point into our heads because he knew it goes against everything you want to believe.

 

[hokie66]

SRE is correct, if he needs any reinforcement. And to me, it is intuitive, rather than otherwise. Hydrostatic pressure depends only on depth, nothing else.

 

[Settingsun]

On the original topic:
Do you only have equivalent fluid pressures from the geotech report? Pretty ordinary report if so.

If you have some geotechnical parameters such as friction angle, cohesion and density, there are ways to calculate a reduced force such as doing a Coulomb wedge analysis and making an estimate of the height that the resultant force acts on the wall. Taking SlideRuleEra's red-line picture a few posts above, you can see that a full active wedge isn't available so the load on the wall is reduced.

Alternatively (or also), there are equations for pressure on silos and bins that take account of the narrow width compared to height.


On the hydrostatic pressure vs width question:
It only depends on fluid density and depth.

However, consider a very narrow pool of water with a limited volume of water (ie doen't get topped up constantly). When the wall moves, the width increases and the water depth reduces...