Triangled
Structural
- Jun 30, 2013
- 594
I'm checking some existing glulams, and, ran across the 1986 NDS commentary on 3.2.1 attached, which as far as I can tell, is still appropriate today. I had overlooked this; it is new to me and puzzles me. I ask your help in understanding and appropriately applying.
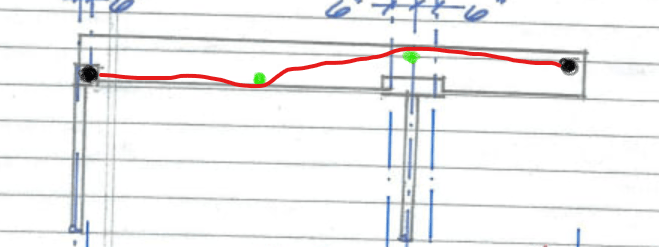
The key item is definition of "span". I am crystal clear for simple span beam. The questions is how to interpret this for cantilevered beam. For years I have adopted the "knife edge" approach at the continuous support. And I do not really understand how to do it any other way. Below the commentary I have appended an sketch illustrating two optional interpretations (perhaps they are both wrong?). Thank you for your consideration.

and here is an illustration showing my dilemma
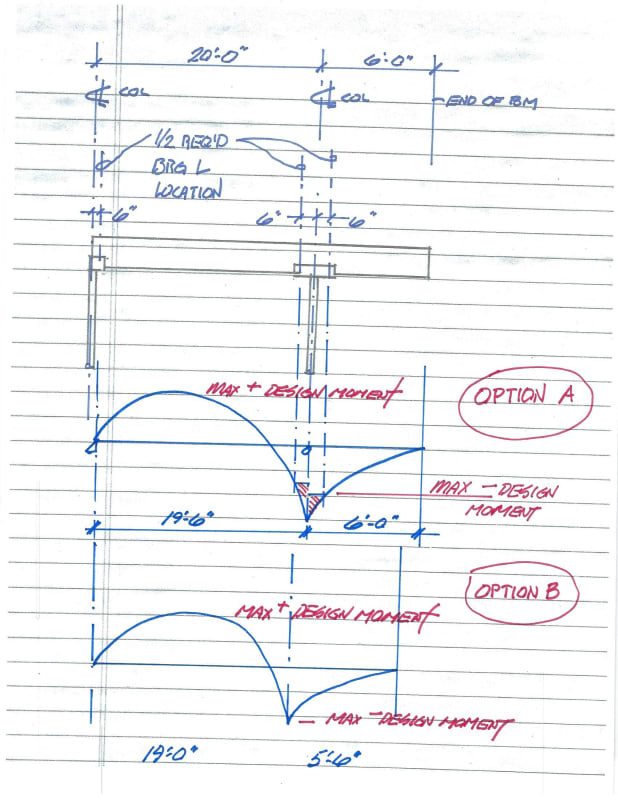
The key item is definition of "span". I am crystal clear for simple span beam. The questions is how to interpret this for cantilevered beam. For years I have adopted the "knife edge" approach at the continuous support. And I do not really understand how to do it any other way. Below the commentary I have appended an sketch illustrating two optional interpretations (perhaps they are both wrong?). Thank you for your consideration.

and here is an illustration showing my dilemma



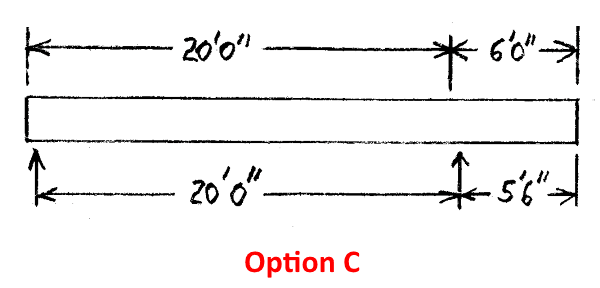
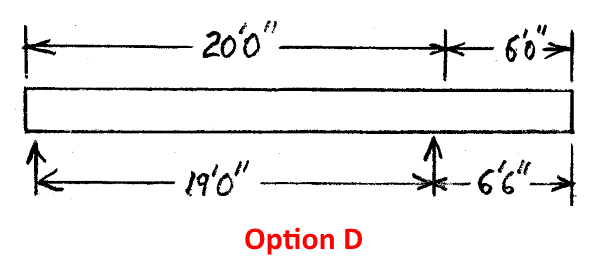
![[idea] [idea] [idea]](/data/assets/smilies/idea.gif)