Pretty Girl
Structural
- Nov 22, 2022
- 148
This is from "Reinforced concrete design to eurocodes" by prab bhat, page 367.
I'm bit confused of how did they determine that this five faced shape has the centroid of 1/3 of the shape's height and breadth.
I feel like they just assumed it's a triangle although the pointy ends are truncated.
I see this as inaccurate to calculate the centroid as we can't be sure the faces of this 5 faced shape (compression block) will be proportional always and the imaginary pointy parts (which extends to the outside of the compression block) of the triangle having same area and size. If it's having the same area, the assumption of the book could be almost correct, but still not entirely correct.
Am I correct or wrong?
If the book has wrong method to find the centroid of this compression block, what are the correct formulas (if any) to find it directly, or your suggestions to find out the centroid of this 5 faced shape.
(the relevant formula part of this problem is highlighted with a pink box below)
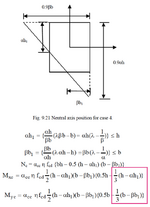
I'm bit confused of how did they determine that this five faced shape has the centroid of 1/3 of the shape's height and breadth.
I feel like they just assumed it's a triangle although the pointy ends are truncated.
I see this as inaccurate to calculate the centroid as we can't be sure the faces of this 5 faced shape (compression block) will be proportional always and the imaginary pointy parts (which extends to the outside of the compression block) of the triangle having same area and size. If it's having the same area, the assumption of the book could be almost correct, but still not entirely correct.
Am I correct or wrong?
If the book has wrong method to find the centroid of this compression block, what are the correct formulas (if any) to find it directly, or your suggestions to find out the centroid of this 5 faced shape.
(the relevant formula part of this problem is highlighted with a pink box below)

