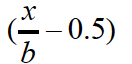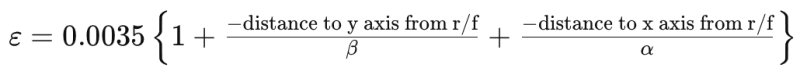Pretty Girl
Structural
- Nov 22, 2022
- 148
I'm trying to understand the concept behind this bi-axial bending calculation. This is from "Reinforced concrete design to eurocodes" by prab bhat, page 368.
I'm bit confused of how the coordinates are calculated for this. For instance, the book states "The bars are located at 0.15h from top and bottom faces and at 0.35b from the sides" and it says b =0.5h.
That means, if we assume the b as 100 mm the height is 200 mm. Now if we try to calculate the distances from top and sides,
If we consider the statement "0.15h from top and bottom faces and at 0.35b from the sides"
right side and left side = 0.35b = 0.35 * 100 = 35 mm
top and bottom distance = 0.15h = 0.15 * 200 = 30 mm
Further it has stated coordinates as (0.2, 0.35)
If we consider that,
the left and right distance = x/b = 0.2, so x = 20 mm.
top and bottom distance = y/h = 0.35, so y distance = 70 mm
So, it confuses me as 35 not equal to 20 mm, neither 30 mm equal to 70 mm.
which one is correct?
If the 35 and 30 mm calculation is correct, then the cordinates of (0.2,0.35) are incorrect isn't it? so the entire strain calculation is incorrect in this book?
If the calculation of the book is incorrect, can you please provide the way to get the strain of each four bars for biaxial bending? I'm trying to create the N-M graph for column design. I referred this book because it aligns with eurocodes and I like the simplicity of the calculations although it's confusing sometimes.

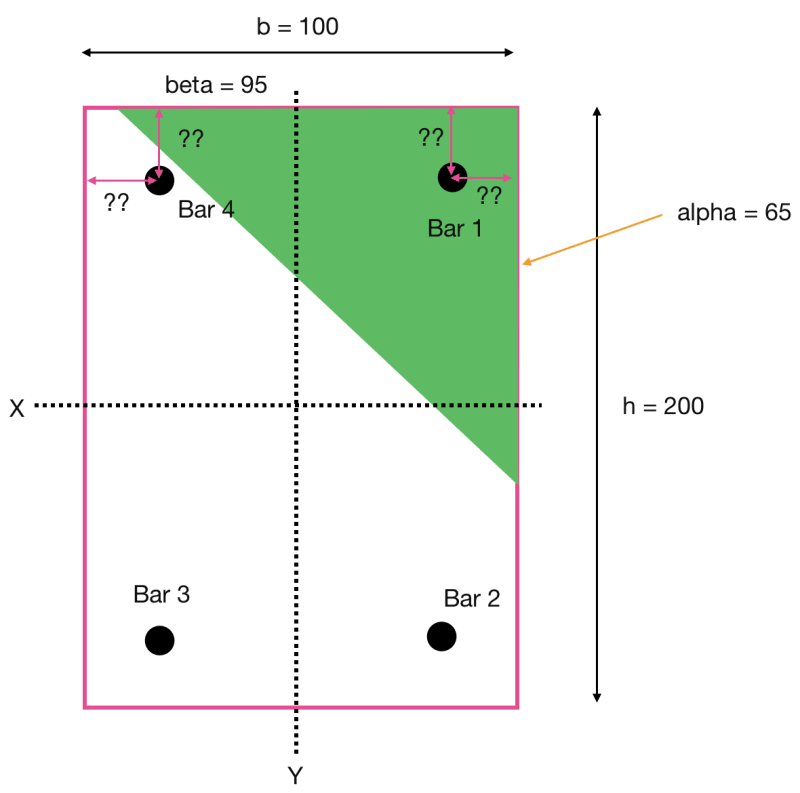
I'm bit confused of how the coordinates are calculated for this. For instance, the book states "The bars are located at 0.15h from top and bottom faces and at 0.35b from the sides" and it says b =0.5h.
That means, if we assume the b as 100 mm the height is 200 mm. Now if we try to calculate the distances from top and sides,
If we consider the statement "0.15h from top and bottom faces and at 0.35b from the sides"
right side and left side = 0.35b = 0.35 * 100 = 35 mm
top and bottom distance = 0.15h = 0.15 * 200 = 30 mm
Further it has stated coordinates as (0.2, 0.35)
If we consider that,
the left and right distance = x/b = 0.2, so x = 20 mm.
top and bottom distance = y/h = 0.35, so y distance = 70 mm
So, it confuses me as 35 not equal to 20 mm, neither 30 mm equal to 70 mm.
which one is correct?
If the 35 and 30 mm calculation is correct, then the cordinates of (0.2,0.35) are incorrect isn't it? so the entire strain calculation is incorrect in this book?
If the calculation of the book is incorrect, can you please provide the way to get the strain of each four bars for biaxial bending? I'm trying to create the N-M graph for column design. I referred this book because it aligns with eurocodes and I like the simplicity of the calculations although it's confusing sometimes.