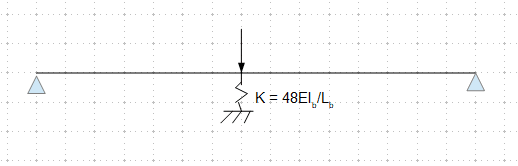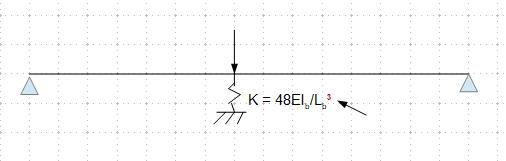hello i am trying to analyze concentrated load on decking to beam force transfer
in particular concentrated load directly over beam
in a previous post someone referred to image below
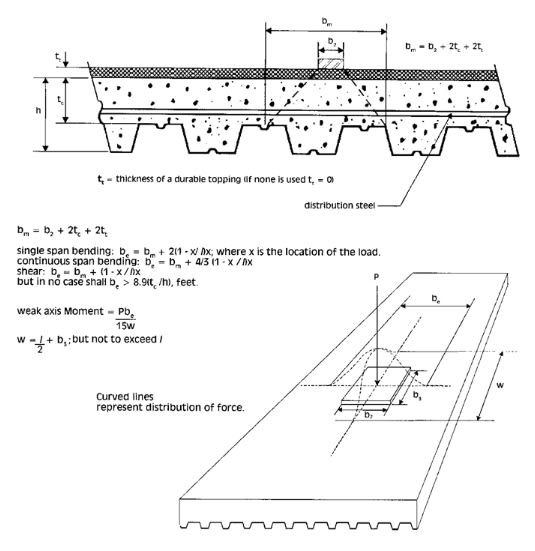
for distribution of concentrated loads for deck slab design
Is it plausible to use the same for force distribution on the supporting beams?
Instead of image below
Perhaps this could be used (image below)
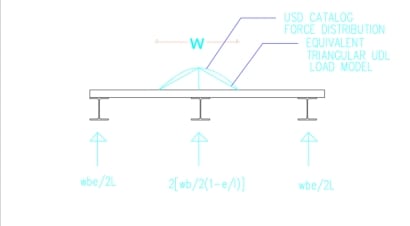
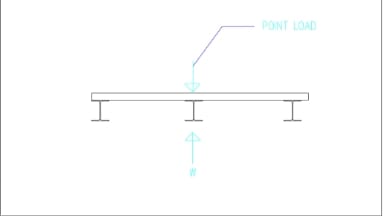
Reference for reaction calcs image below
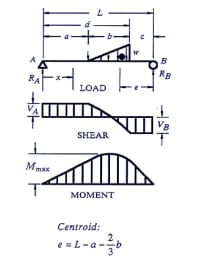
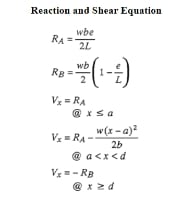
Also could you refer to further calculation to incorporate the stiffness of the slab into spreading to adjacent supporting beams
in the scenario of concentrated load directly on top of the beam?
in particular concentrated load directly over beam
in a previous post someone referred to image below

for distribution of concentrated loads for deck slab design
Is it plausible to use the same for force distribution on the supporting beams?
Instead of image below

Perhaps this could be used (image below)

Reference for reaction calcs image below

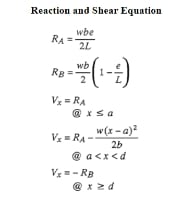
Also could you refer to further calculation to incorporate the stiffness of the slab into spreading to adjacent supporting beams
in the scenario of concentrated load directly on top of the beam?