fa2070
Structural
- Jun 6, 2007
- 58
Hi,
This is a conceptual question on reinforced concrete design.
Given an arbitrary cross section subjected to a normal force F and a bending moment M (see picture), how do I tackle its design? Is it a beam with a normal force or is it a column with a bending moment? How do I tell?
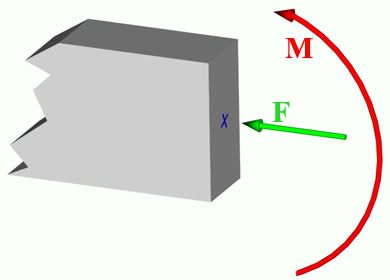
Thanks.
This is a conceptual question on reinforced concrete design.
Given an arbitrary cross section subjected to a normal force F and a bending moment M (see picture), how do I tackle its design? Is it a beam with a normal force or is it a column with a bending moment? How do I tell?

Thanks.
