EngRepair said:
I'm quite surprised if you're not recognizing that this is the same question, not a new one.
Additionally, I didn't see any specific answers to my last, very straightforward questions.
So, could you clarify if it's possible to use a 50 HP motor winding in a 60 HP pump motor?
I already asked for clarification on your "very straightforward questions" in my post 15 Mar 23 13:10.
EngRepair said:
I have some experience as a winder, but I'm not particularly fond of theory.
Take the theory at whatever level you are comfortable. Ask questions. If there is a disagreement, that's a time to be even more skeptical and ask more questions.
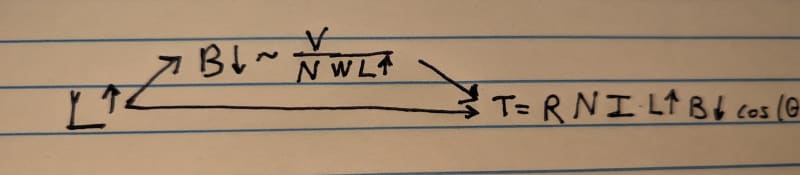
If you reject any reference to theory then what's left... intuition? Does it pass your intuition test when someone claims to you that T ∝ B I
independent of length? So if we have a loop carrying current I in a field B, the torque is the same REGARDLESS of the length? A one meter long loop sees the same torque as a 10 meter long loop? I'd think that would set off some intuitive alarm bells for you.
edison said:
Quote (T = B I cosɸ R N L Kdp... is an equality)
That's not the torque equation, that's emf equation sans the PF & I.
So, your whole argument(s) in this thread is/are based on a false equation and hence not worthy of consideration.
It
is the torque equation. There's nothing to do with emf anywhere in sight there. I'm not sure what you're looking at.
The full derivation of the torque equation quoted above (excluding Kdp) is given in the attachment to my post dated 7 Mar 23 14:21, starting from first principles F= q*velocity x B =L I x B (with suitable background to explain why force on conductor equation gives the correct result).
And it matches a textbook equation that I also referenced in that attachment except the textbook equation adds the Kdp)
The equation is important. It's at the center of our disagreement.
I have already invited you to provide an alternate equation but you have not. I assume you understand the difference between an equation and a proportionality.
Let me ask the same question in a different way. if I told you the air gap flux, the current in the slot conductors, and the total number of conductors, how would you quantitatively estimate the numerical value of the torque? feel free to identify additional parameters needed to support the calculation. I claim the additional parameters needed are the ones that I already said in the equation you quoted.
This is an important question and I would like for you to not ignore it. you can look it up in a textbook.
if you don't have a textbook, there's a shortcut that will get you there which is to look at the
units of the variables.
B has units of Tesla = volt*sec / m^2
B x I has units of (volt*sec / m^2) *A = (A*volt)*sec/m^2 = (watt*sec)/m^2 = Joule/m^2 = N-m / m^2 = N/m
Newton/m... that sounds like force per length.
(And indeed that's what we already knew since F = qVx B = I L x B, so F / L = I x B.... so I x B gives force per length. Yup.)
If I had a loop I might be interested in the torque. So I'd multiply by the radius.
R*F / L = T / L = R * I B
The units are now newton-meter per meter. Torque per length on a loop. Sounds kind of like what Bill was talking about.
I wonder how we would convert FROM torque per length TO torque. Multiply by length maybe? Apparently you don't think so. I'll be interested to see how you make the units work out when you answer the question of how to quantitatively estimate torque.
To recap I am waiting for one or both of the following:
[ul]
[li]1. What
equation would you propose to use for torque instead of the equation that I provided?[/li]
[li]2. If you had to quantitatively estimate torque developed by a given motor given B and I, tell me how you would do it, including what other parameters would you need. (Are you
really sure you don't need L?)[/li]
[li]3. EDIT - BONUS QUESTION. Let's say I have 2 loops carrying the same current in the same field, each one similar to
this. The only difference between the two loops is that one is 1m long and the other is 10m long. Does the 10m loop experience the same torque as the 1m loop? (PS - if you are looking for R and L within the link I just posted earlier in this bullet, they are hidden in area A = 2 R L)[/li]
[/ul]