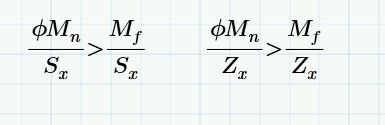Flexural Strength Using Elastic Distribution 6

[CDLD]

Hello everyone,

The current AISC A360-16 Spec calculates flexural strength based on plastic section properties for the most part.
If you wanted to calculate the flexural strength based on the principles of elastic distribution how would you manipulate the equations provided in chapter F2 (doubly symmetric i-shapes)to do this (A360-16)

Do you agree with the following?

1. Yielding. Mn = Mp = Fy*Sx

2.Lateral torsional buckling.

Lp<Lb<Lr (inelastic buckling)
Mn = cb[Fy*Sx - (0.3 FySx)*((Lb-Lp)/(Lr-Lp))]< Fy*Sx (similar to provisions in chapter F5)

Lb>Lr (elastic buckling)
no changes.

The reason why I am curious is because, the code recommends using elastic distribution when combining flexure and torsion.

 

[IDS]

It doesn't cover torsional warping's effect on the stiffness of WF and channels. However, it points to some reference papers on the subject. I haven't read them. But, they sound like what is needed for one of these programs to really do warping correctly.

It does give a complete stiffness matrix for beam elements including warping terms, so that can be used to analyse the effect of torsional warping on any section, including WF and channels.

I did quite a bit of work on this last year, including comparing my own frame analysis spreadsheet results (using the stiffness matrix from the book) with analyses in Mastan and also FEA analyses with beams built up from plate elements. Results from all three were in pretty good agreement, and significantly different from a frame analysis without warping effects, especially for short members.




Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[IDS]

I've got that one (hard copy even) and used it extensively in grad school. Does it actually cover the torsion business?

The pdf version on the Mastan site is Version 2, so if your hard copy is Ver. 1 it would be worth downloading the later one.

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[CDLD]

3) The second term of the equation supports my position on this in that Fbx encompasses the beam LTB check calculated in the normal manner, with Mp rather than My.

Any idea why, this equation from design guide 9 allows you to design to Mp in the strong-axis, but only My in the weak-axis?

This doesn't seem right to me.

 

[JoshPlumSE]

Any idea why, this equation from design guide 9 allows you to design to Mp in the strong-axis, but only My in the weak-axis?

My sense is that because the torsional warping stresses create a stress profile akin to weak axis bending, they're being a little more conservative with those stresses.... Using 0.60Fy instead of 0.66 or 0.75Fy.

 

[KootK]

I disagree with that step on two fronts:

1) It's logically inconsistent to calculate an LTB capacity using plastic principles and then prorate it with an elastic section modulus. Again with the apples and oranges.

2) It overestimates capacity. Since Zx > Sx, dividing by Sx will actually inflate the critical buckling stress in a way that is inappropriate.

So I think that I've gotten myself right with that bit of it. I believe that the key to it is to realize what must happen when you eventually compare the "buckling stress" to something as shown below. Whether you take the path on the left or the path on the right, it cancels out to being just the moment capacity. So, as long as one is consistent, the choice of Sx or Zx makes no difference. And, given that the idea is to do everything else in terms of Sx, sure, why not do this in terms of Sx too?

The whole concept of a "buckling stress" is really a bit misleading. In terms of simplified, code bifurcation buckling checks, the parameter of interest is stiffness and not stress. We've only jury rigged the equation in terms of stress in the past so as to make the whole thing more comfortable for folks used to working with rudimentary, mechanics of materials stress equations. Obviously, one can say that a thing buckles at a particular stress but that's a derived parameter, not a fundamental one. I'd be thrilled to see this step in DG09 skipped altogether and just left at Mn.

 

[KootK]

Any idea why, this equation from design guide 9 allows you to design to Mp in the strong-axis, but only My in the weak-axis?

I've got nothing any more definitive than JP's explanation. I agree, it does seem inconsistent.