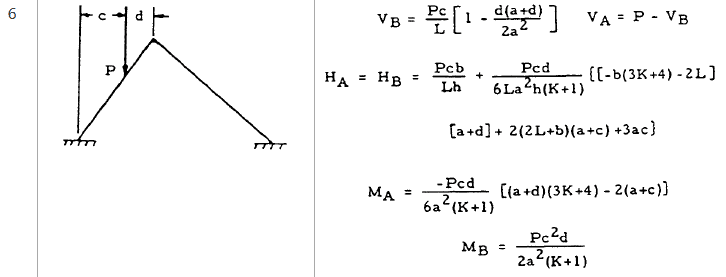AwesomeAndy3
Civil/Environmental
Hi everyone,
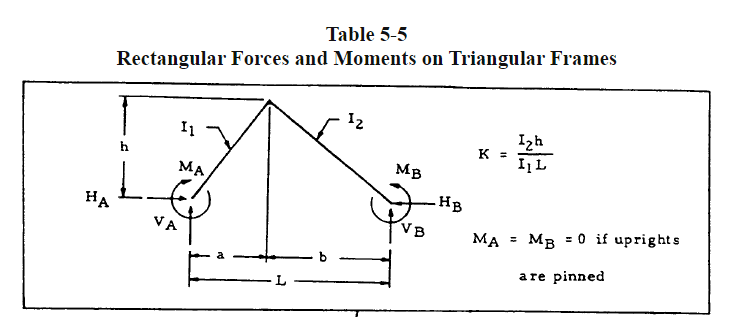
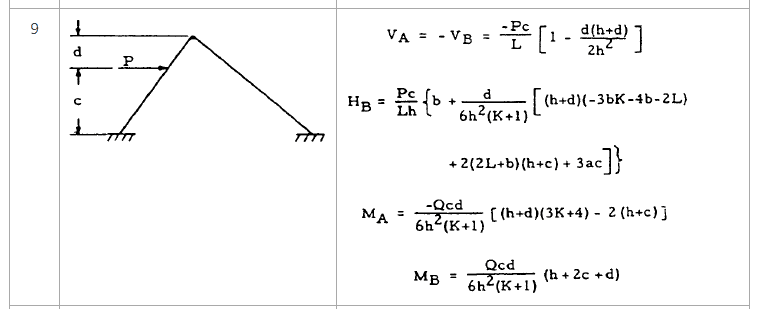
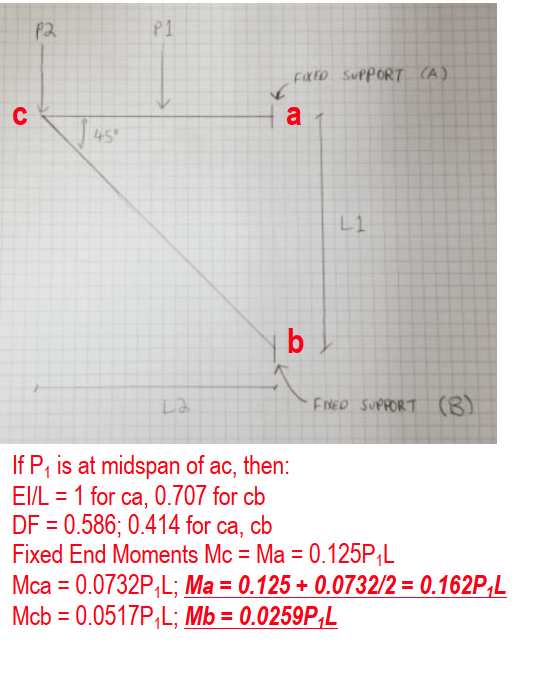
I hope this is the right place to post this question, but I'm wondering if the free body diagram below can be solved? Or would it be indeterminate?
See below for picture. The two beams are angle irons.
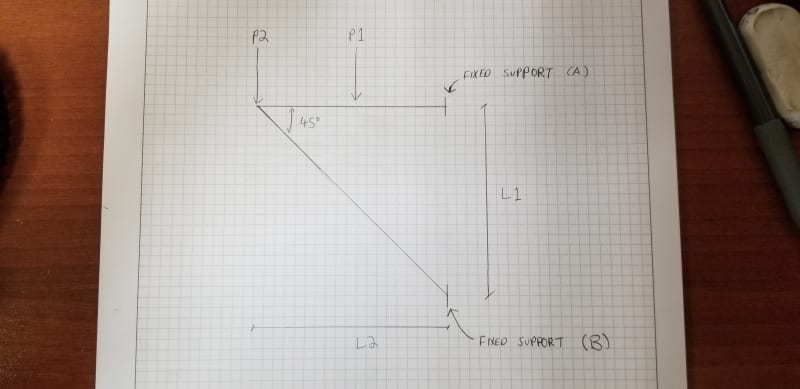
Assuming I know values for forces P1 and P2, lengths L1 and L2, is there a way to calculate the reaction forces and moments at fixed supports A and B?
Any help is greatly appreciated.
Thanks,
I hope this is the right place to post this question, but I'm wondering if the free body diagram below can be solved? Or would it be indeterminate?
See below for picture. The two beams are angle irons.

Assuming I know values for forces P1 and P2, lengths L1 and L2, is there a way to calculate the reaction forces and moments at fixed supports A and B?
Any help is greatly appreciated.
Thanks,