Julian2w2w
Mechanical
- Jun 2, 2020
- 17
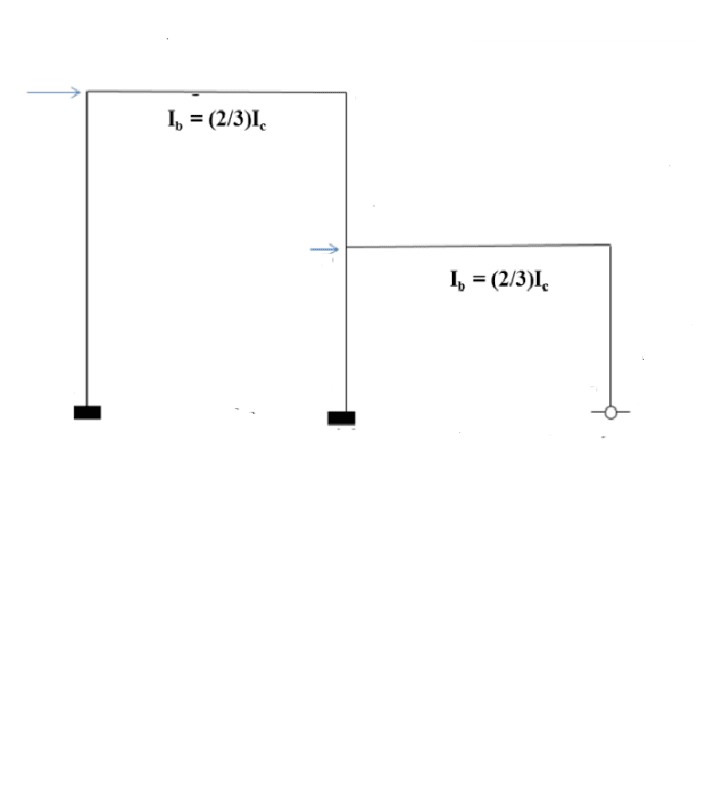
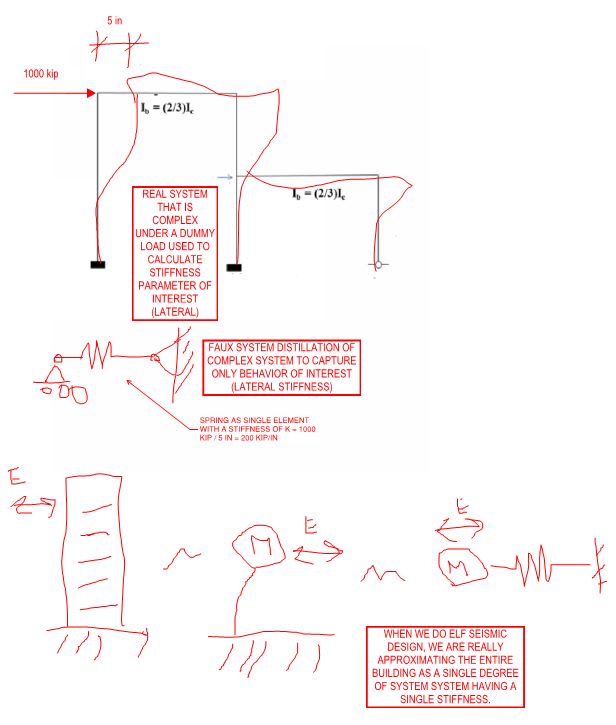
Hox can a frame have a single element to represent its overall stiffness?
I found that in a book. From what I remember, a single-storey or double or multi-storey have a matrix of stiffness.
Only a structural member can have one element to represent its stiffnees?
I found that in a book. From what I remember, a single-storey or double or multi-storey have a matrix of stiffness.
Only a structural member can have one element to represent its stiffnees?