Eurotex
Mechanical
- Sep 14, 2020
- 11
CAUTION: This post uses the ISO GPS system of geometric dimensioning and tolerancing
Can the parallelism tolerance shown in the below image (with respect to common datum A-B) be considered to control coaxiality of the A and B diameters? If so, would you assume the equivalent coaxiality/position tolerance to be 0.005?
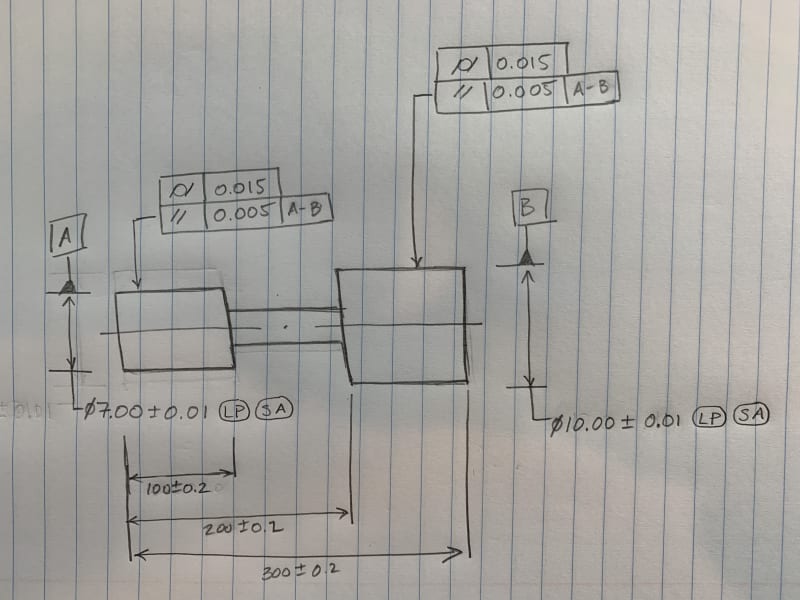
Can the parallelism tolerance shown in the below image (with respect to common datum A-B) be considered to control coaxiality of the A and B diameters? If so, would you assume the equivalent coaxiality/position tolerance to be 0.005?

