DCBII
Structural
- Apr 15, 2010
- 187
I'm a full time engineer, but I've put together a sort of hobby computer program that does basic finite element analysis to help me learn how it works. I've been trying to add MITC4 elements for linear analysis (nothing too fancy) but I'm having some trouble. This is my first time creating isoparametric elements, so I'm learning.
I've modeled a 10' wide x 20' tall x 1' thick concrete rectangular wall panel (E = 3823 ksi, nu=0.17) fixed on on four sides with a uniform surface pressure of 250 psf. I've meshed it incredibly fine with 6"x6" rectangular plates.
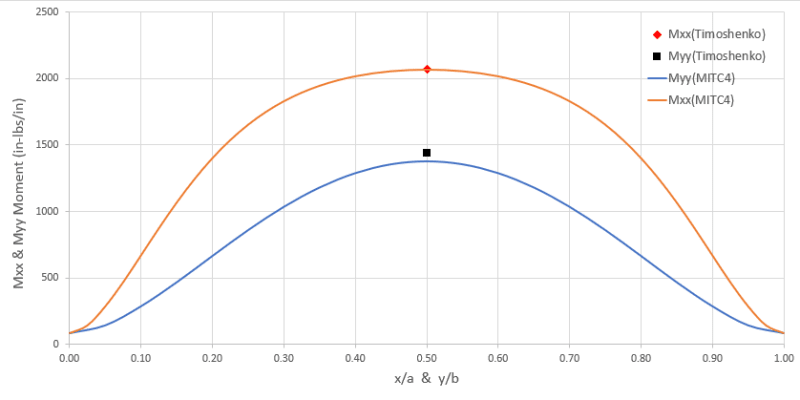
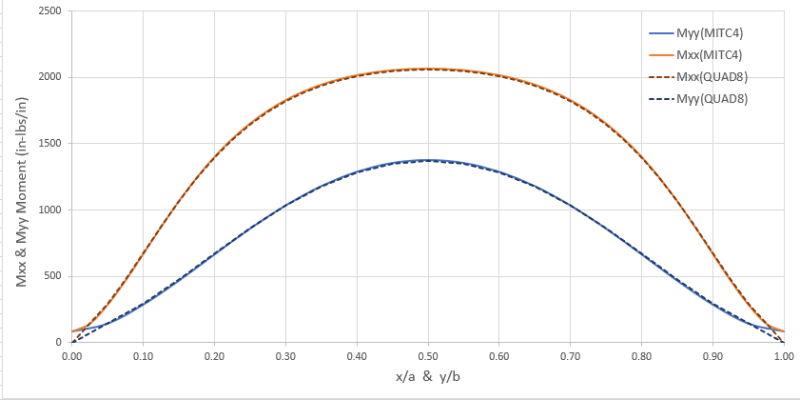
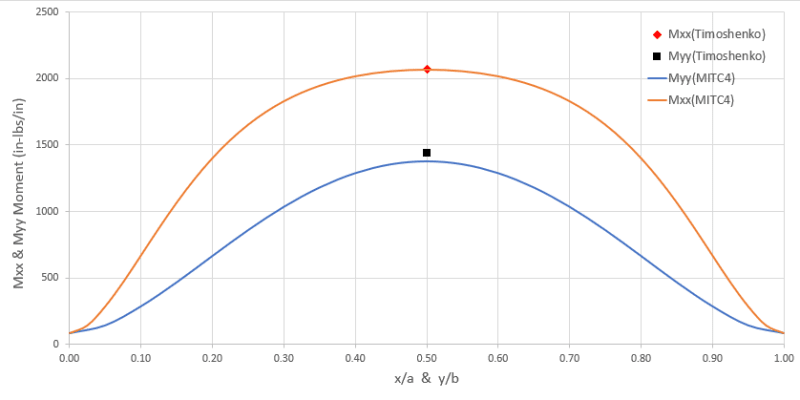
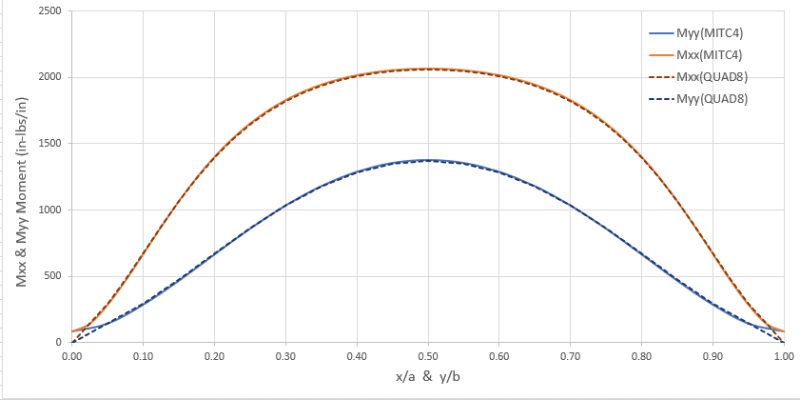
The shear stresses my model is calculating are spot on with values published by Timoshenko in "Theory of Plates and Shells", but the bending stresses that are calculated are about 15% smaller. The displacement calculated at the center of the panel is also slightly larger (~10%) than Timoshenko predicts. I've plotted contours and the displaced shape and the shape of the bending moment, and they both look correct. Only the magnitudes appear to be slightly off. The excess deflection and low moments make me think my flexural stiffness is too low, but my stress-strain matrix [Cb] is the easiest matrix to calculate and I've checked it multiple times.
I've calculated my stresses as [Mx, My, Mxy] = [Cb][d], with calculated at the 2x2 gauss integration points (+/-0.5773). I then extrapolated those stresses to the nodes using the shape functions. The extrapolation made very little difference with such a fine mesh, as the stress is nearly constant over the plate's area at locations of maximum moment. I don't think my extrapolation is the problem.
Any finite element geniuses out there with an idea what might be going on here? Do MITC4 bending elements require me to mesh even finer? My slow personal computer might blow up if I do. That seems like extremely poor convergence.
I've modeled a 10' wide x 20' tall x 1' thick concrete rectangular wall panel (E = 3823 ksi, nu=0.17) fixed on on four sides with a uniform surface pressure of 250 psf. I've meshed it incredibly fine with 6"x6" rectangular plates.
The shear stresses my model is calculating are spot on with values published by Timoshenko in "Theory of Plates and Shells", but the bending stresses that are calculated are about 15% smaller. The displacement calculated at the center of the panel is also slightly larger (~10%) than Timoshenko predicts. I've plotted contours and the displaced shape and the shape of the bending moment, and they both look correct. Only the magnitudes appear to be slightly off. The excess deflection and low moments make me think my flexural stiffness is too low, but my stress-strain matrix [Cb] is the easiest matrix to calculate and I've checked it multiple times.
I've calculated my stresses as [Mx, My, Mxy] = [Cb][d], with calculated at the 2x2 gauss integration points (+/-0.5773). I then extrapolated those stresses to the nodes using the shape functions. The extrapolation made very little difference with such a fine mesh, as the stress is nearly constant over the plate's area at locations of maximum moment. I don't think my extrapolation is the problem.
Any finite element geniuses out there with an idea what might be going on here? Do MITC4 bending elements require me to mesh even finer? My slow personal computer might blow up if I do. That seems like extremely poor convergence.