skewl
Structural
- Jul 27, 2021
- 46
Based on the Canadian codes (A23.3 / S6), moment resistance of a concrete beam can be found by determining "c", finding the equivalent rectangular stress block, and obtaining the compression forces in the concrete. This is all fine for a rectangular beam with the same concrete material. However, what do you do in situations where the concrete beam has two different compressive strengths?
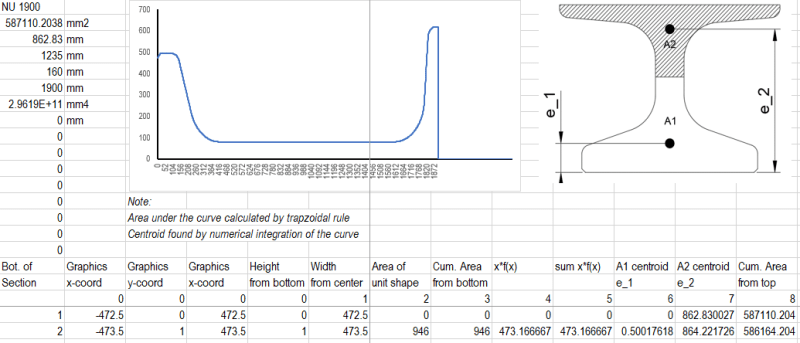
For example, I have a 50MPa pretensioned NU girder acting compositely with a 30MPa deck slab. The N.A. of the composite section ("c") is within the web on the girder so both types of concrete are engaged. In this case:
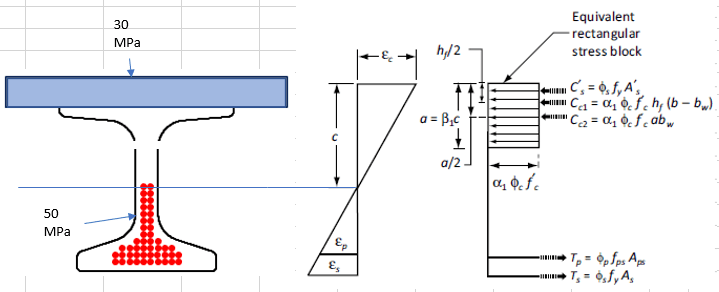
1) How do you determine "a" (i.e. a = beta*c)? The alpha and beta factor is dependent on the material properties of the concrete (i.e. beta = 0.97-0.0025*f'c).
2) My understanding of the beta factor is that it converts the "non-uniform stress block" acting on a rectangular section to an "equivalent rectangular stress block" acting on a rectangular section. The NU girder is not a rectangular section and its width varies non-linearly with depth. Is it still correct to apply the beta factor to "c" to find "a" in this case?
3) My current approach is to transform the width of the deck slab by n = Ec,g / Ec,s (like what you would do in a steel-concrete composite beam), and then assuming f'c = 50MPa in all my calculations.
Unfortunately my company doesn't have software to do pretensioned beam design so I am unable to verify my calculations with a computer program. Any advice/literature on this is appreciated.
For example, I have a 50MPa pretensioned NU girder acting compositely with a 30MPa deck slab. The N.A. of the composite section ("c") is within the web on the girder so both types of concrete are engaged. In this case:
1) How do you determine "a" (i.e. a = beta*c)? The alpha and beta factor is dependent on the material properties of the concrete (i.e. beta = 0.97-0.0025*f'c).
2) My understanding of the beta factor is that it converts the "non-uniform stress block" acting on a rectangular section to an "equivalent rectangular stress block" acting on a rectangular section. The NU girder is not a rectangular section and its width varies non-linearly with depth. Is it still correct to apply the beta factor to "c" to find "a" in this case?
3) My current approach is to transform the width of the deck slab by n = Ec,g / Ec,s (like what you would do in a steel-concrete composite beam), and then assuming f'c = 50MPa in all my calculations.

Unfortunately my company doesn't have software to do pretensioned beam design so I am unable to verify my calculations with a computer program. Any advice/literature on this is appreciated.


![[bigsmile] [bigsmile] [bigsmile]](/data/assets/smilies/bigsmile.gif) . Thank you again for your help!
. Thank you again for your help!