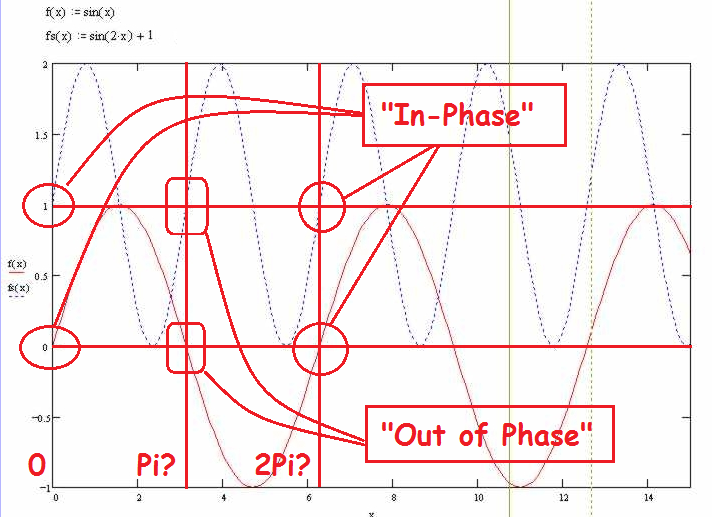
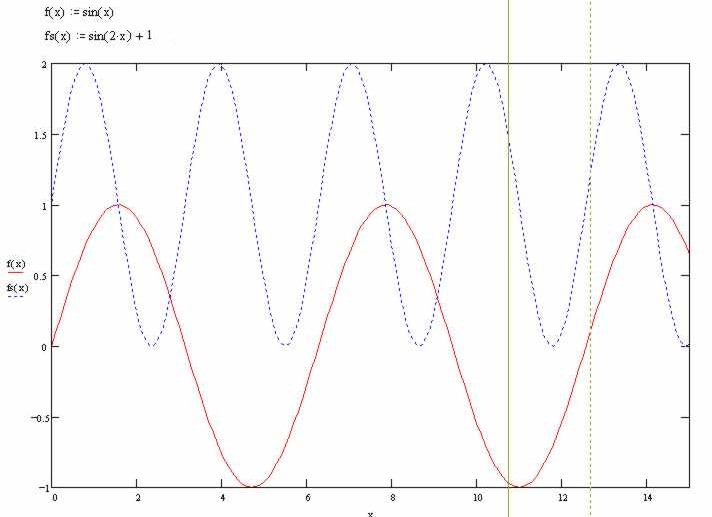
I have a sine wave plotted, i.e. y = sin(x)
I have a second wave plotted, where y = sin(2x)+1
I now wish to introduce a phase shift, such that the latter wave becomes tangential with the former.
Whether the shift is in the X+ or X- direction is irrelevant to me.
Can anyone please explain how to calculate this phase shift, and illustrate it with an Excel graph, to show that the results of the calculation actually do provide the correct phase shift to create the condition where the waves are actually tangential at certain periodic instants.
Thanks
I have a second wave plotted, where y = sin(2x)+1

I now wish to introduce a phase shift, such that the latter wave becomes tangential with the former.
Whether the shift is in the X+ or X- direction is irrelevant to me.
Can anyone please explain how to calculate this phase shift, and illustrate it with an Excel graph, to show that the results of the calculation actually do provide the correct phase shift to create the condition where the waves are actually tangential at certain periodic instants.
Thanks