Navigation
Install the app
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
More options
Style variation
-
Congratulations cowski on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Punching shear with 2 way moment
- Thread starter Smoulder
- Start date
- Status
- Not open for further replies.
Usually you just superimpose the stresses from axial, and both orthogonal moments to find the maximum around the column perimeter. Then compare this to max allowable stresses as per your code. This is a fairly universal approach in international concrete codes.
I know ACI codes for punching shear (ACI 421 series) have some particular guidance for punching shear in PT slabs, cannot recall the differences as been a few years since I used them, but from memory you can rely on some additional component due to any precompression. If you can get a copy they are a good resource for all aspects of punching shear, complete with examples.
I know ACI codes for punching shear (ACI 421 series) have some particular guidance for punching shear in PT slabs, cannot recall the differences as been a few years since I used them, but from memory you can rely on some additional component due to any precompression. If you can get a copy they are a good resource for all aspects of punching shear, complete with examples.
- Thread starter
- #3
Thanks Agent666. I olny have the main ACI318 code not the one you said for PT slabs. But I looked it up for reinforced slabs and it has a diagram showing the shear stress varies around the punching cone perimeter similar to P/A+My/I so pretty easy just to add the second direction's moment as you said. That would give max shear stress at one corner, min at the opposite corner, and in between on the other two corners.
But AS3600 seems to have a different method and it's not easy to follow just based on the code and commentary as it rolls up the formula into sort of a reduction factor for moment compared to the zero moment case. Not stresses like ACI. So I dug my old textbook out of storage over the long weekend and it looks like the stress distribution is different to ACI. The front face seems to have the average shear stress while the side faces vary linearly due to shear+torsion so the shear stress at the corners is different depending on which face you're looking at.
The textbook also answers my question by saying "The values of M*v inthe x and y directions are usually different. The values of a are also different if the column is nt square. In using Eq 19.28 the greater of the two values of M*v/a is employed." So you don't add them but just take whichever is worst and this is what I thought based on the commentary but it seemed unconservative. Maybe because AS3600 is conservative compared to ACI which is why you don't add? AS3600 takes 80% of the moment as side torsion causing additional shear stress (40% each side) with 20% as direct moment on the front face which doesn't increase shear stress. ACI says 40% as additional shear spread around all four sides and 60% as direct moment.
But AS3600 seems to have a different method and it's not easy to follow just based on the code and commentary as it rolls up the formula into sort of a reduction factor for moment compared to the zero moment case. Not stresses like ACI. So I dug my old textbook out of storage over the long weekend and it looks like the stress distribution is different to ACI. The front face seems to have the average shear stress while the side faces vary linearly due to shear+torsion so the shear stress at the corners is different depending on which face you're looking at.
The textbook also answers my question by saying "The values of M*v inthe x and y directions are usually different. The values of a are also different if the column is nt square. In using Eq 19.28 the greater of the two values of M*v/a is employed." So you don't add them but just take whichever is worst and this is what I thought based on the commentary but it seemed unconservative. Maybe because AS3600 is conservative compared to ACI which is why you don't add? AS3600 takes 80% of the moment as side torsion causing additional shear stress (40% each side) with 20% as direct moment on the front face which doesn't increase shear stress. ACI says 40% as additional shear spread around all four sides and 60% as direct moment.
- Thread starter
- #4
Here are 2 pages from the textbook. The first shows the force distribution around the cone and the second shows how the code equation 19.26/28 relates to stresses. The stress equation isn't in the code or commentary. You can see in figure 19.6 equations that all the moment is direct moment on the front/back faces or torsion on the side faces unlike ACI.
Safe to follow the book and check the two directions separately?
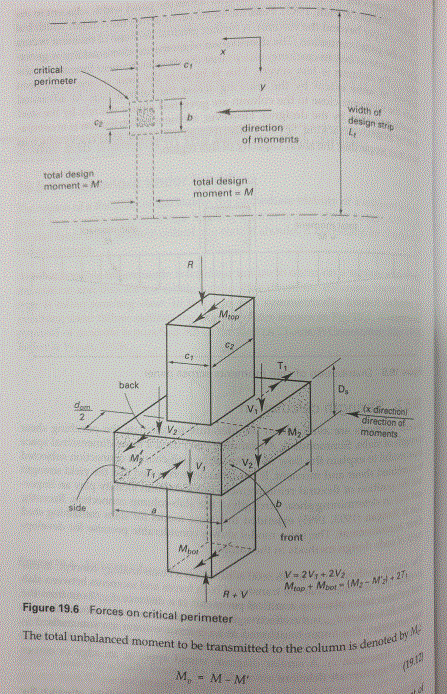

Safe to follow the book and check the two directions separately?


Yeah I see it works quite a bit differently having now flicked through the code (I'm more familiar with ACI, NZS3101).
I think because it's working out a capacity based on the applied moment and shear I think the way I'd look at it would be to work out the critical stress from the combined moments, and equate that stress back to an equivalent moment about the one axes to evaluate the critical capacity Vu depending on what scenario governed your situation from 9.3.4.
But if the textbook is saying just take the worst M*v/a then I guess that's the code writers intent. But I fail to see how those capacity equations really take account of a situation like in figure 9.3(A)(a) with an L shaped column where the principal axes don't align with the applied moment. The only logical way to assess that situation is to work out the properties of the critical section and superimpose stresses I would have thought.
Though despite what the text says I'd also run the numbers on the ACI stress route, as seems like the most logical way to allow for the effects of any post tensioning if not explicitly accounted for in AS3600. That is effectively going to work out a limiting stress, to which you compare your calculated stresses. That seems more fundamentally correct to me when there is limited ability for redistribution to occur. Although once you've required reinforcement for shear using shear reinforcement or stud rails, there is according to ACI standards some ability to achieve some level of ductility.
I think because it's working out a capacity based on the applied moment and shear I think the way I'd look at it would be to work out the critical stress from the combined moments, and equate that stress back to an equivalent moment about the one axes to evaluate the critical capacity Vu depending on what scenario governed your situation from 9.3.4.
But if the textbook is saying just take the worst M*v/a then I guess that's the code writers intent. But I fail to see how those capacity equations really take account of a situation like in figure 9.3(A)(a) with an L shaped column where the principal axes don't align with the applied moment. The only logical way to assess that situation is to work out the properties of the critical section and superimpose stresses I would have thought.
Though despite what the text says I'd also run the numbers on the ACI stress route, as seems like the most logical way to allow for the effects of any post tensioning if not explicitly accounted for in AS3600. That is effectively going to work out a limiting stress, to which you compare your calculated stresses. That seems more fundamentally correct to me when there is limited ability for redistribution to occur. Although once you've required reinforcement for shear using shear reinforcement or stud rails, there is according to ACI standards some ability to achieve some level of ductility.
It's also not apparent to me how 9.3.4 is supposed to take account of edge and corner conditions?
Again going the stress route explicitly accounts for the discontinuities in the crticial perimeter. Those 9.3.4 equations seem like they only cover the most idealised situations (single axis moment on rectangular interior column), anything else seems to be lacking specific advice on how to undertake the assessment. Fundamentally to me you could have the same moment/shear, same perimeter length and end up with the same capacity. But in reality that critical perimeter could be any shape but the same length, so there is a fundamental disconnect to me when you relate it back to a stress on critical perimeter scenario
Again going the stress route explicitly accounts for the discontinuities in the crticial perimeter. Those 9.3.4 equations seem like they only cover the most idealised situations (single axis moment on rectangular interior column), anything else seems to be lacking specific advice on how to undertake the assessment. Fundamentally to me you could have the same moment/shear, same perimeter length and end up with the same capacity. But in reality that critical perimeter could be any shape but the same length, so there is a fundamental disconnect to me when you relate it back to a stress on critical perimeter scenario
rapt said:The 2 directions are done independently, as they are in ACI318.
I don't really agree with that statement. The intent of ACI318 with respect to punching shear is that the stresses are additive for each orthogonal bending axis (edit: if there are concurrent bending actions). It's more clearly stated in ACI421.1 than ACI318, it's one of those things ACI318 probably doesn't explicitly state. But it becomes fairly clear if you think about what's going on that axial and both moments need to be considered concurrently otherwise you're undercooking the design.
This is from ACI421.1 which is referenced from ACI318 for further clarification on punching shear matters.

I guess you're in a better place than me to try explain why AS3600 thinks considering concurrent moments independently is considered acceptable.
I would have thought the wording in ACI318 R8.4.4.2.3 says it.
"The maximum factored shear stress may be calculated from"
and it provides a unidirectional calculation.
This has been discussed several times in other threads.
As the current Australian code method relies purely on the torsional capacity of the transverse torsion strip, I cannot see how it can logically be based on a combined M!
"The maximum factored shear stress may be calculated from"
and it provides a unidirectional calculation.
This has been discussed several times in other threads.
As the current Australian code method relies purely on the torsional capacity of the transverse torsion strip, I cannot see how it can logically be based on a combined M!
- Thread starter
- #10
Thanks again, good discussion.
@Agent666 Is there an appendix B in ACI421 that says 15% overstress when checking moment in two directions? I found that on a web search but looked a bit old and maybe meant old version of ACI421. It said checking each direction seperately is usual because different load patterns needed to get max moment.
I also think AS3600 sitrrups for punching will be wider than ACI because trying to fill the torsion strip instead of concentrate near the column. Are both wide and narrow stirrups valid?
@Agent666 Is there an appendix B in ACI421 that says 15% overstress when checking moment in two directions? I found that on a web search but looked a bit old and maybe meant old version of ACI421. It said checking each direction seperately is usual because different load patterns needed to get max moment.
I also think AS3600 sitrrups for punching will be wider than ACI because trying to fill the torsion strip instead of concentrate near the column. Are both wide and narrow stirrups valid?
Designing for a single orthogonal momemt for punching shear in isolation would be like only designing a column for each orthogonal moment in isolation. Hey might work sometimes depending on how hard things are working relative to real biaxial capacity, other times not so much if you were to look at both moments concurrently.
I believe it's one of those cases you're always referring to regarding code gives you some rules, but cannot cover every eventuality and you have to apply these rules logically knowing what you know about the principles involved. To me that is considering the stresses as being additive like explicitly explained in ACI421.1. It probably helps from my perspective in making this leap because its taught this way in universities (here at least) as the way to get it done.
Now having said all that I did find this in PCA notes document for 2011 version of ACI318 (the reference it is referring to dates from 1973 though, some knowledge moves on), but it is in contrast to what ACI421.1 2020 version requires.

I freely admit the aussie way of evaluating this makes absolutely no sense to me at all having lived the ACI/NZS life for 20 odd years. I guess someone did some research into it at some point to ensure it meets the required safety indices and its another route to demonstrate adequacy.
However the lack of information on how edge and openings are accounted for in those prebaked capacity equations has me baffled. It suggests two perimeters of the same length are equal in capacity despite the potentially for the critical perimeter to be significantly different configurations. To me and my brain that seems fundamentally an issue as the stresses involved around two different perimeters have obvious risks of being quite different, yet the same capacity according to AS3600 provisions. But i guess I'm coming at it from never having used these provisions in anger to understand if they are more or less conservative than the ACI stress based approach which is obviously backed by a large body of research and testing.
I believe it's one of those cases you're always referring to regarding code gives you some rules, but cannot cover every eventuality and you have to apply these rules logically knowing what you know about the principles involved. To me that is considering the stresses as being additive like explicitly explained in ACI421.1. It probably helps from my perspective in making this leap because its taught this way in universities (here at least) as the way to get it done.
Now having said all that I did find this in PCA notes document for 2011 version of ACI318 (the reference it is referring to dates from 1973 though, some knowledge moves on), but it is in contrast to what ACI421.1 2020 version requires.

I freely admit the aussie way of evaluating this makes absolutely no sense to me at all having lived the ACI/NZS life for 20 odd years. I guess someone did some research into it at some point to ensure it meets the required safety indices and its another route to demonstrate adequacy.
However the lack of information on how edge and openings are accounted for in those prebaked capacity equations has me baffled. It suggests two perimeters of the same length are equal in capacity despite the potentially for the critical perimeter to be significantly different configurations. To me and my brain that seems fundamentally an issue as the stresses involved around two different perimeters have obvious risks of being quite different, yet the same capacity according to AS3600 provisions. But i guess I'm coming at it from never having used these provisions in anger to understand if they are more or less conservative than the ACI stress based approach which is obviously backed by a large body of research and testing.
@Agent666 Is there an appendix B in ACI421 that says 15% overstress when checking moment in two directions? I found that on a web search but looked a bit old and maybe meant old version of ACI421. It said checking each direction seperately is usual because different load patterns needed to get max moment.
There is an appendix B in parts .1 & .2, but neither make mention of that overstress, but it is inferred that if you've reinforced for shear that some ductility can be accommodated without a brittle failure occurring.
I think ACI does kind of cover it if you consider their terminology, they just discuss an unbalanced moment, not a specific unidirectional moment. They just give one example for calculating the stresses that happens to be uni-directional.
The AS3600 rules are based on testing done by Rangan in the 1980's.
But they do cover edge and corner column situations are covered in the code.
I am not saying I like them. Currently trying to change the method for the next AS3600 revision.
The ACI method is empirical. The method was developed to use for uni-directional effects. Otherwise you would have to determine Polar moment of inertia at the angle of the Moment resultant to do it properly and no-one was going to do that without a computer.
Earlier AS codes had the ACI method, and I still like it, but not sure what the new method will be yet. Argument against it is that is is not how punching shear really works. But as a dumb engineer it seems a logical approach to me and presumably others.
But they do cover edge and corner column situations are covered in the code.
I am not saying I like them. Currently trying to change the method for the next AS3600 revision.
The ACI method is empirical. The method was developed to use for uni-directional effects. Otherwise you would have to determine Polar moment of inertia at the angle of the Moment resultant to do it properly and no-one was going to do that without a computer.
Earlier AS codes had the ACI method, and I still like it, but not sure what the new method will be yet. Argument against it is that is is not how punching shear really works. But as a dumb engineer it seems a logical approach to me and presumably others.
- Thread starter
- #14
Nothing to add except I wish I'd read the textbook and not posted. No offence intended, just it's now complicated in my mind. Will probably try ACI if a complex geometry comes up so doubling workload.
Here's the full textbook section for Agent666 and anyone else interested.
And thanks again!




Here's the full textbook section for Agent666 and anyone else interested.
And thanks again!




- Status
- Not open for further replies.
Similar threads
- Question
- Replies
- 29
- Views
- 29K
- Locked
- Question
- Replies
- 1
- Views
- 365
- Locked
- Question
- Replies
- 29
- Views
- 5K
- Locked
- Question
- Replies
- 57
- Views
- 4K
- Locked
- Question
- Replies
- 27
- Views
- 4K
