MacGruber22
Structural
- Jan 30, 2014
- 802
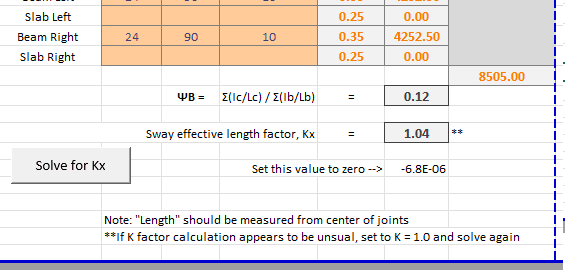
Has anyone ever tried turning the alignment chart into an excel spreadsheet that allows direct calculation rather than graphically drawing a line between ΨA, ΨB, and K?
RAM concrete does not automatically account for p-delta in concrete columns. This necessitates a hand calc check on whether columns are sway or not, and then hand calc to determine K.
-Mac
RAM concrete does not automatically account for p-delta in concrete columns. This necessitates a hand calc check on whether columns are sway or not, and then hand calc to determine K.
-Mac