Antidude90
Structural
- Feb 9, 2024
- 13
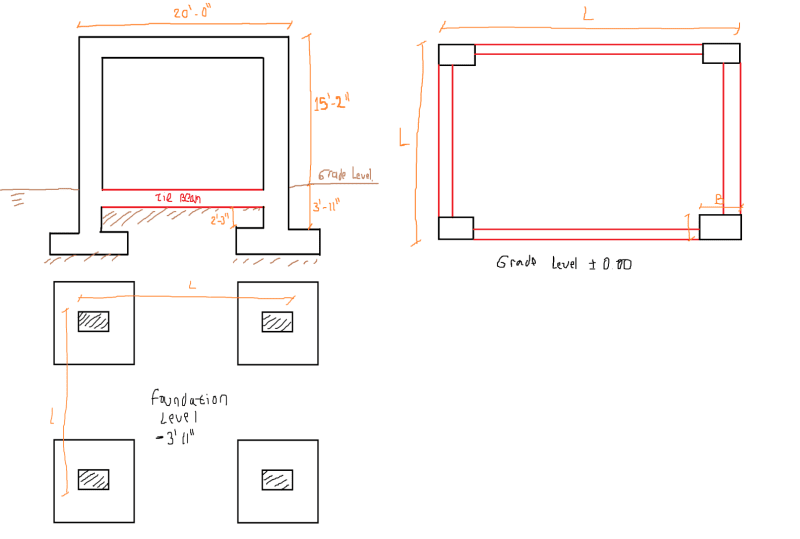
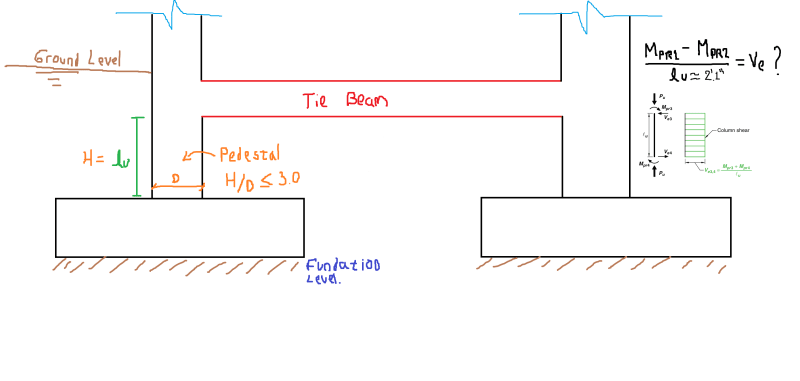
I have a moment-resisting concrete frame structure located in a high seismic hazard zone. At the base or ground level, I will place a tie beam that will be connected to pedestals (or fully buried column sections that allow the foundation level to be reached) (see attached image).
Considering that the pedestals comply with the H/d < 3.0 ratio, and taking into account the provisions of ACI 318 18.2.2.3, which states that "any element below the base required to transmit seismic forces must comply with the provisions of Chapter 18", I'm wondering follow:
- Should the pedestal be considered as an element subjected to axial load and bending, as those defined in 18.7?
- If so, should the design shear force (Ve) be satisfied, as described in 18.7.6.1, where the shear force must be calculated considering the maximum probable moments at the faces of the joints and the unsupported length of the pedestals!!!?
- In my opinion, it is not necessary to calculate the design shear force in the pedestal as if it were expected to dissipate energy. Because the pedestal, being buried and having a low H/d ratio (less than 3), behaves more like a rigid body than a flexible element. Also,the main function of the pedestal is to transmit the axial force of the column to the ground and the shear force transfer between the pedestal and the ground is mainly done by friction. In my experience, I have designed pedestals in this way without performing the design shear force calculation as defined in 18.7.6.1, and I have not found any problems.
I appreciate any comments or suggestions you may have regarding this.
Considering that the pedestals comply with the H/d < 3.0 ratio, and taking into account the provisions of ACI 318 18.2.2.3, which states that "any element below the base required to transmit seismic forces must comply with the provisions of Chapter 18", I'm wondering follow:
- Should the pedestal be considered as an element subjected to axial load and bending, as those defined in 18.7?
- If so, should the design shear force (Ve) be satisfied, as described in 18.7.6.1, where the shear force must be calculated considering the maximum probable moments at the faces of the joints and the unsupported length of the pedestals!!!?
- In my opinion, it is not necessary to calculate the design shear force in the pedestal as if it were expected to dissipate energy. Because the pedestal, being buried and having a low H/d ratio (less than 3), behaves more like a rigid body than a flexible element. Also,the main function of the pedestal is to transmit the axial force of the column to the ground and the shear force transfer between the pedestal and the ground is mainly done by friction. In my experience, I have designed pedestals in this way without performing the design shear force calculation as defined in 18.7.6.1, and I have not found any problems.

I appreciate any comments or suggestions you may have regarding this.